Обчислити площу фігури D, яка обмежена параболою \(y=x^2-2x\) та прямою \(y=x\).
Розв'язання:
Побудуємо фігуру D за рівняннями її межі (рис. 1).

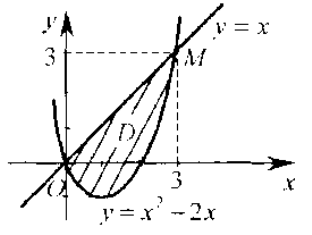
Розв'язавши систему рівнянь $$\begin{cases} y=x^2-2x & \\ y=x& \ \end{cases}$$
Знайдемо, що \(x_1=0,\;x_2=3; \; y_1=0,\; y_2=3\) відповідно.
Отже, лінії, що обмежують область, перетинаються в точках \(O(0,0)\) та \(M(3,3)\).
Область D задається системою нерівностей: $$D:\;0\leq x\leq 3,\; x^2-2x\leq y\leq x.$$
Тоді $$S={\int \int}_{D} {dxdy}=\int_{0}^{3}{dx}\int_{x^2-2x}^{x}{dy}=\int_{0}^{3}(x-x^2+2x)dx=$$ $$=\left(\frac{3}{2}x^2-\frac{x^3}{3} \right)\mid _{0}^{3}=\frac{9}{3}.$$

---