Вычислить объем тела, ограниченного параболоидом z = 2 − x2 − y2
и конической поверхностью
\(z=\sqrt{x^2+y^2}\).
Исследуем сначала пересечение двух заданных поверхностей. Приравнивая координаты z, получаем уравнение \(2-x^2-y^=\sqrt{x^2+y^2}\)
Пусть x2 + y2 = t2. Тогда
\(2-t^2=t\) или \(t^2+t-2=0 \Rightarrow t 1,2=\frac{-1\pm 3}{2}=-2,1\)
В контексте данной задачи смысл имеет лишь корень t = 1, то есть
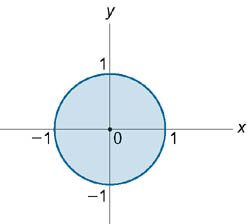
\(z=\sqrt{x^2+y^2}=1\) или \(x^2+y^2=1\)Итак, обе поверхности пересекаются при z = 1, и сечение представляет собой круг (рисунок 1.1)
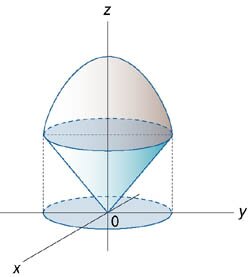
Область интегрирования сверху ограничена параболоидом , а снизу − конусом (рисунок 1.2). Для вычисления объема области перейдем
к цилиндрическим координатам:
\(x^2+y^2=\rho ^2, \sqrt{x^2+y^2}=\rho , dxdydz=\rho d\rho d\varphi dz\)
В результате находим
\(V=\int \int \int_{V}{\rho d\rho d\varphi dz}=\int_{0}^{2\pi }{d\varphi
}\int_{0}^{1}{\rho d\rho }\int_{\rho }^{2-\rho ^2}{dz}=\)
\(=\int_{0}^{2\pi }{d\varphi }\int_{0}^{1}{\rho d\rho }\cdot (2-\rho
^2-\rho )=\int_{0}^{2\pi }{d\varphi }\int_{0}^{1}{(2\rho -\rho ^3-\rho
^2)}d\rho =\)
\(=\int_{0}^{2\pi }{d\varphi }=\left[\left(\rho ^2-\frac{\rho^4
}{4}-\frac{\rho ^3}{3} \right)\mid_{0}^{1} \right] =\int_{0}^{2\pi}
\left(1-\frac{1}{4}-\frac{1}{3} \right){}d\varphi =\)
\(=\frac{5}{12}\int_{0}^{2\pi }{d\varphi }=\frac{5\pi }{6}\)
Ответ: \(=\frac{5}{12}\int_{0}^{2\pi }{d\varphi }=\frac{5\pi }{6}\)
Пример 2:
Вычислить объем тела, ограниченного поверхностями $$y^2=x, x=3, z=x, z\geq 0$$
Решение:
Данное тело ограничено сверху плоскостью z = x (рисунок 1.3), поэтому его объем определяем следующим образом:
\(\int \int_{D}{xdxdy}=2\int_{0}^{\sqrt{3}}{dy}\int_{y^2}^{3}{xdx} =2\int_{0}^{\sqrt{3}}{(\frac{x^2}{2}}\mid_{y^2}^{3}\) dy=
\(=2\int_{0}^{\sqrt{3}}{(\frac{9}{2}-\frac{y^2}{2})dy}=2(\frac{9}{2\sqrt{3}}-\frac{9\sqrt{3}}{10})=\frac{36\sqrt{2}}{5}\)
Рисунок 1.3
Ответ: \(\frac{36\sqrt{2}}{5}\) (куб.ед)
2012-12-25 • Просмотров [ 11700 ]