Що розуміють під кутом між прямою і площиною?
Якщо пряма паралельна або належить площині, то вважають, що кут між такою прямою і площиною дорівнює \(0^{\circ}\). Якщо пряма перпендикулярна до площини, то кут між ними дорівнює \(90^{\circ}\). У решті випадків кутом між прямою і площиною називають кут між прямою і її проекцією на площину.

Задача №764

З однієї точки до площини проведено дві рівні похилі. Кут між ними \(60^{\circ}\), а між їхніми проекціями \(90^{\circ}\). Знайдіть кути між проекціями і площіною.

Розв'язання

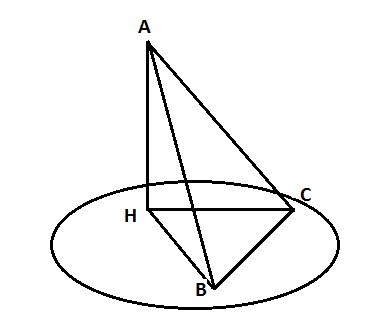
\(AB=AC,\)
\(\angle{BAC}=60^{\circ}\), отже, \(\triangle{ABC}\) - правильний, \(ВС=AВ,\).
\[HB=\sqrt{AB^{2}-AH^{2}}=\sqrt{AC^{2}-AH^{2}}=HC\]
\(\triangle{HBC}\) - прямокутний,
\[BC^{2}=HB^{2}+HC^{2}=2HB^{2},\]
\[AB^{2}=2HB^{2}, HB=\frac{\sqrt{2}}{2}AB=HC.\]
\[\cos\angle{ABH}=\frac{HB}{AB}=\frac{\sqrt{2}}{2},\angle{ABH}=45^{\circ}.\]
\[\cos\angle{ACH}=\frac{HC}{AC}=\frac{HB}{AB}=\frac{\sqrt{2}}{2},\]
\[\cos\angle{ACH}=\cos\angle{ABH}=45^{\circ}\]

Відповідь:\(45^{\circ}\)

Задача №770

Знайдіть кут між бічним ребром і площиною основи правильного тетраедра.

Розв'язання
Позначимо О- ценрт \(\triangle{АBC}\), тоді \(DO\bot{(ABC)}\).

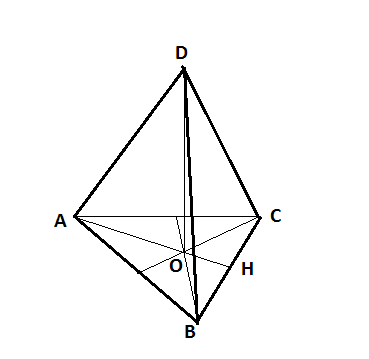
Нехай АВ=а, АН - висота, медіана і бісектриса \(\triangle{АBC}\), АО:ОН=2:1.
\[AO=\frac{2}{3}AH, AH=\frac{\sqrt{3}}{2}a, AO=\frac{\sqrt{3}}{3}a\]
\[\cos\angle{DAO}=\frac{OA}{AD}=\frac{\frac{\sqrt{3}}{3}a}{a}=\frac{\sqrt{3}}{3}\]
\[\angle{DAO}=\arccos{\frac{\sqrt{3}}{3}}\]

Відповідь: \(\arccos{\frac{\sqrt{3}}{3}}\)

Умови задач взято з підручника "Геометрія 10 клас" (Бевз, Владімірова).

---