Приближенные методы интегрирования. Продолжение. Начало здесь
Пример 2. Вичислим приближенное значение интеграла $$I=\int_{0}^{\pi }{\sin xdx}=2.$$
Пусть \(n=6\). Тогда по формуле трапеций $$I\approx I_{mp}=\frac{\pi }{6}(\frac{\sin 0+\sin \pi }{2}+\sin \frac{\pi }{6}+\sin \frac{2\pi }{6}+\sin \frac{3\pi }{6}+\sin \frac{4\pi }{6}+\sin \frac{5\pi}{6})=\frac{\pi }{6}(0,5+\frac{1}{2}\sqrt{3}+1+\frac{1}{2}\sqrt{3}+0,5)=1,9541.$$
Абсолютная ошибка равна \(0,0459\), а относительная - \(2,5\%\).
В этом примере подынтегральная функция в интервале интегрирования не монотонна и мы не можем дать оценку для вычисляемого интеграла.
Действительно, здесь \(\underline{I}=\overline{I}=I_{mp}\), т.е. все эти значеия дают искомую величину интеграла с недостатком. Чтобы получить все-таки оценку для вычисляемого интеграла, мы должны разбить интервал интегрирования на части, в каждой из которых функция монотонна, и рассмотреть интегралы по каждому частичному интервалу отдельно.
II. Правило Симпсона. Это правило требует не намного большей затраты труда, чем предыдущие, а приводит обычно к более точным результатам (при одном и том же разбиении интервала).
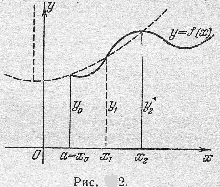
Как и раньше, разобьем интервал \([a,b]\) на \(n\) равных частей, но предполпожим, что \(n\) - четное число: \(n=2m\). Заменим дугу линии \(y=f(x)\), соответствующую интервалу \([x_{0}, x_{2}]\), дугой параболы, ось которой параллельна оси ординат и которая проходит через следующие три точки дуги: начальную точку дуги \((x_{0}, y_{0})\), среднюю точку \((x_{1}, y_{1})\), конечную точку \((x_{2}, y_{2})\) (рис.2). Аналитически, это означает, что в интервале \([x_{0}, x_{2}]\) данная функция \(y=f(x)\) заменяется квадратичной функцией \(y=px^{2}+qx+r\). Коэффициенты \(p\), \(q\) и \(r\) выбираются так, чтобы значения обеих функций были равны при \(x_{0}\), \(x_{1}\) и \(x_{2}\) соответственно
|
$$y_{0}=px_{0}^{2}+qx_{0}+r,$$
|
$$y_{1}=px_{1}^{2}+qx_{1}+r,$$
|
$$y_{2}=px_{2}^{2}+qx_{2}+r.$$
|
Решая полученные уравнения, находим коэффициенты \(p\), \(q\) и \(r\).
Произведя подобные замены и в интервалах \([x_{2}, x_{4}]\), \([x_{4}, x_{6}]\),...,\([x_{n-2}, x_{n}]\) будем считать, что площадь данной трапеции приближенно равна сумме площадей получающихся параболических трапеций. Докажем теперь, что площадь \(S\) трапеции, ограниченной какой-нибудь параболой \(y=px^{2}+qx+r\) с осью, параллельной оси ординат, будет выражаться формулой
|
$$S=\frac{L_{osn}}{6}(y_{n}+4y_{c}+y_{k}),$$
|
(1) |
Предположим сначала, что основанием трапеции служит интервал оси \(Ox\), симметричный относительно начала координат, \([-\gamma,\gamma]\). Для площади такой параболической трапеции имеем выражение $$S=\int_{-\gamma }^{\gamma }{(px^{2}+qx+r)dx}=p\int_{-\gamma }^{\gamma }{x^{2}dx}+q\int_{-\gamma }^{\gamma }{xdx}+r\int_{-\gamma }^{\gamma }{dx},$$
т.е. $$S=p\frac{\gamma ^{3}-(-\gamma )^{3}}{3}+q\frac{\gamma ^{2}-(-\gamma )^{2}}{2}+r\frac{\gamma -(-\gamma )}{1}=\frac{2}{3}p\gamma ^{3}+2r\gamma.$$
Так как здесь \(y_{n}=y_{x=-\gamma }=p\gamma ^{2}-q\gamma +r,\) \(y_{c}=y_{x=0}=r,\) \(y_{k}=y_{x=\gamma }=p\gamma ^{2}+q\gamma +r\) и длина основания равна \(2\gamma\), то непосредственной подстановкой этих значений в формулу (1) убеждаемся в ее справедливости.
Очевидно, что эта формула справедлива и для параболической трапеции рассматриваемого вида с любым основанием. Действительно, площадь трапеии не изменится, если перенести ее параллельно самой себе так, чтобы основание стало симметричным относительно начала координат, и тогда искомая площадь выразится в согласии с формулой (1).
Возвращаясь к первоначальной задаче, найдем по этой формуле площадь \(S_{1}\) параболической трапеции, опирающейся на интервал \([x_{0}, x_{2}]\): $$S_{1}=\frac{x_{2}-x_{0}}{6}(y_{0}+4y_{1}+y_{2})=\frac{\Delta x}{3}(y_{0}+4y_{1}+y_{2}),$$
где \(\Delta x=\frac{b-a}{n}\). Аналогично выразятся площади \(S_{2}, S_{3}, ... , S_{m}\) последующих параболических трапеций:
|
$$S_{2}=\frac{\Delta x}{3}(y_{2}+4y_{3}+y_{4}),$$
|
|
$$S_{3}=\frac{\Delta x}{3}(y_{4}+4y_{5}+y_{6}),$$
|
|
.............................
|
|
$$S_{m}=\frac{\Delta x}{3}(y_{n-2}+4y_{n-1}+y_{n}).$$
|
Сложив почленно все эти равенства, получим выражение, дающее приближенное значение искомого интеграла: $$I\approx \frac{\Delta x}{3}[y_{0}+4y_{1}+2y_{2}+4y_{3}+2y_{4}+...+4y_{n-1}+y_{n}].$$
Это и есть формула Симпсона.
По формуле Симпсона, например, для интеграла \(I=\int_{0}^{1}{x^{4}dx}\) (\(=0,2\)) при \(n=10\) находим: \(I\approx 0,200013\); абсолютная ошибка составляет всего \(0,000013\), а относительная - \(0,01\%\).
Ясно, что для любого интеграла от квадратичной функции \(y=px^{2}+qx+r\) формула Симпсона должна, конечно, дать точное значение. Заметим, что формула Симпсона дает также точное значение и для интеграла от кубической функции.
Приближенные методы интегрирования. Продолжение здесь