Производная от интеграла по его верхнему пределу.
I. Интеграл с переменным верхним пределом. Будем считать нижний предел интеграла постоянным, а верхний переменным. Придавая верхнему пределу различные значения, будем получать соответствующие значения интеграла; следовательно, при рассматриваемом условии интеграл является функцией своего верхнего предела.
Независимая переменная в верхнем пределе обычно обозначается той же буквой, скажем \(x\), что и переменная интегрирования. Таким образом, например, записывают $$I(x)=\int_{a}^{x}{f(x)dx}.$$
Однако переменная \(x\) в подынтегральном выражении служит лишь вспомогательной переменной - переменной интегрирования, пробегающей в процессе составления интеграла (суммирования) значения от \(a\) до \(x\) - верхнего предела интеграла. Если нам нужно вычислить частное значение функции \(I(x)\), например при \(x=b\), т.е. \(I(b)\), то мы подставим \(b\) вместо \(x\) в верхний предел интеграла, но, разумеется, не будем подставлять \(b\) вместо переменной интегрирования. Поэтому нагляднее было бы употреблять такую запись: $$I(x)=\int_{a}^{x}{f(t)dt},$$
взяв для переменной интегрирования какую-нибудь другую букву (здесь \(t\)).
Свойства интеграла относятся и к интегралу с переменным верхним пределом.
II. Производная от интеграла. Весьма важно изучить связь между функцией \(I(x)\) и данной подынтегральной функцией \(f(x)\).
Теорема о производной интеграла по верхнему пределу. Производная от интеграла по его верхнему пределу равна подынтегральной функции
|
$$I'(x)=(\int_{a}^{x}{f(x)dx})'=f(x).$$
|
(1) |
Иными словами: интеграл с переменным верхним пределом является первообразной для подынтегральной функции.
Доказательство. Придадим аргументу \(x\) приращение \(\Delta x\). Тогда наращенное значение функции \(I(x)\) будет $$I(x+\Delta x)=\int_{a}^{x+\Delta x}{f(x)dx}.$$
Значит, $$\Delta I=I(x+\Delta x)-I(x)=\int_{a}^{x+\Delta x}{f(x)dx}-\int_{a}^{x}{f(x)dx}.$$
Применяя к первому интегралу справа теорему о разбиении интервала интегрирования, получим $$\Delta I=\int_{a}^{x}{f(x)dx}+\int_{x}^{x+\Delta x}{f(x)dx}-\int_{a}^{x}{f(x)dx}=\int_{x}^{x+\Delta x}{f(x)dx}.$$
Последний интеграл по теореме о среднем равен $$\Delta I=f(\xi )(x+\Delta x-x)=f(\xi )\Delta x,$$
где \(\xi\) - точка, лежащая между \(x\) и \(x+\Delta x.\)
По определению производной имеем $$I'(x)=\lim_{\Delta x\rightarrow 0}\frac{\Delta I}{\Delta x}=\lim_{\Delta x\rightarrow 0}\frac{f(\xi )\Delta x}{\Delta x}=\lim_{\Delta x\rightarrow 0}f(\xi ).$$
Но если \(\Delta x\rightarrow 0\), то \(x+\Delta x\) стремится к \(x\); поэтому и подавно \(\xi\rightarrow x\), а так как \(f(x)\) - непрерывная функция, то $$\lim_{\Delta x\rightarrow 0}f(\xi )=\lim_{\xi \rightarrow x}f(\xi )=f(x),$$
что и требовалось доказать.
Из теоремы также следует, что
|
$$d\int_{a}^{x}{f(x)dx}=f(x)dx.$$
|
(2) |
Необходимо заметить, что результаты в формулах (1) и (2) не зависят от обозначения переменной интегрирования; имеют место, например, такие равенства:
|
$$\frac{d}{dx}\int_{a}^{x}{f(t)dt}=f(x),$$
|
$$d\int_{a}^{x}{f(t)dt}=f(x)dx.$$
|
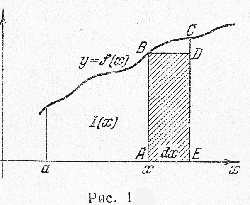
Геометрический смысл теоремы. Функция \(I(x)\) выражает переменную площадь криволинейной трапеции с переменным основанием \([a,x]\), ограниченной линией \(y=f(x)\). В теореме утверждается, что производная от площади трапеции по абсциссе равна ординате линии, ограничивающей трапецию (отрезок \(AB=f(x)\) на рис.1), или что дифференциал площади трапеции равен площади прямоугольника \(ABDE\) со сторонами, равными соответственно приращению основания трапеции и ординате линии в крайней точке.