Уранвнение вида

$$P(x,y)dx+Q(x,y)dy=0$$

называется однородным, если \(P(x,y)\) и \(Q(x,y)\) - однородные функции одного измерения. Функция \(f(x,y)\) называется однородной измерения \(m\) ,если

$$f(\lambda x,\lambda y)=\lambda ^mf(x,y)$$

Однородное уравнение может быть приведено к виду \(y^{'}=f(y/x)\) . С помощью подстановки \(y=tx\) однородное уравнение приводится к уравнению с разделяющимися переменными по отношению к новой неизвестной функции \(t\) .

Пример 1. Найти общий интеграл уравнения

$$(x^2+2xy)dx+xydy=0$$

Здесь \(P(x,y)=x^2+2xy,Q(x,y)=xy.\) Обе функции - однородные второго измерения. Введем подстановку \(y=tx,\) откуда \(dy=xdt+tdx\). Тогда уравнение примет вид

$$(x^2+2x^2t)dx+tx^2(xdt+tdx)=0$$

или

$$(x^2+2x^2t+t^2x^2)dx+tx^3dt=0.$$

Разделяя переменные и интегрируя, имеем

$$\frac{dx}{x}+\frac{tdt}{(t+1)^2}=0;\int \frac{dx}{x}+\int \frac{tdt}{(t+1)^2}=C.$$

Преобразуем второй интеграл:

$$\ln \left|x \right|+\int \frac{t+1-1}{(t+1)^2}dt=C$$

или

$$\ln \left|x \right|+\ln \left|t+1 \right| \frac{1}{t+1}dt=C.$$

Возвращаясь к прежней неизвестной функции \(t\) \((y=y/x)\) , получаем окончательный ответ :

$$\ln \left|x+y \right|+\frac{x}{x+y}=C.$$

Пример 2. Найти частное решение уравнения \(y^{'}=\frac{y}{x}+\sin\frac{y}{x}\) при начальном условии \(y(1)=\pi /2\) .

Произведем подстановку \(y/x=t\) , откуда \(y=tx,\) \(dy=xdt+tdx.\) . В результате получаем

$$xdt+tdx=(t+\sin t)dx;xdt=\sin tdx; \frac{dt}{\sin t}=\frac{dx}{x}.$$

Интегрируя имеем

$$\ln \left|tg(t/2) \right|=\ln \left|x \right|+\ln C, (t/2=arctg(Cx)).$$

Производя обратную замену \(t=y/x,\) находим общее решение исходного уравнения. Используя заданное начальное условие, получим \(\pi /2=2x\)\(arctg(Cx)\) , откуда \(C=1\) .

Итак, искомое частное решение имеет вид \(y=2xarctgx\).

Пример 3. Найти кривую, проходящую через точку \(A(0;1)\) , для которой треугольник, образованный осью \(Oy\), касательной к кривой в произвольной ее точек и радиусом - вектором точки касания, - равнобедренный (причем основанием его служит отрезок касательной от точки касания до оси \(Oy\)).

Пусть \(y=f(x)\) - искомое уравнение кривой. Проведем касательную \(MN\) в произвольной точке \(M(x,y)\) кривой до пересичения с осью \(Oy\) в точке \(N\) .

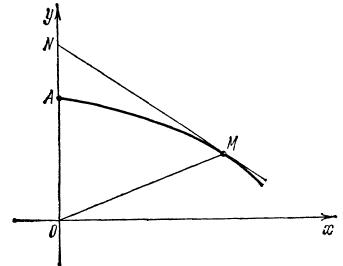
Согласно условию, должно выполнятся неравнество \(\left|ON \right|=\left|OM \right|.\) Но \(\left|OM \right|=\sqrt {x^2+y^2}\), а \(\left|ON \right|\) найдем из уравнения касательной \(Y-y=y^{'}(X-x)\) полагая \(X=0\) , т.е. \(Y=\left|ON \right|=y-xy^{'}\).

Итак, приходим к однородному уравнению

$$\sqrt {x^2+y^2}=y-xy^{'}.$$

Полагая \(y=tx\), после замены и разделения переменных получим

$$\frac{dt}{\sqrt {1+t^2}}=-\frac{dx}{x}$$

или

$$\ln (t+\sqrt {1+t^2})=\ln C-\ln x$$

откуда \(x^2=C(C-2y)\)

Подставляя координаты точки \(A\) в найденное общее решение, получим \(0=C(C-2);\) из двух значений \(C=0,C=2\) годится лишь второе, поскольку при \(C=0\) парабола выражается в оси \(Oy\). Итак, искомой кривой является парабола \(x^2=4(1-y)\) \(y=1-x^2/4\).или

2012-12-16 • Просмотров [ 4574 ]