Струной называется тонкая нить, котрая может свободно изгибатся. Пусть струна находится под действием сильного начального натяжения \(T_0\) . Если вывести стуну из положения равновесия и подвергнуть действию какой-нибудь силы, то струна начнет колебаться.

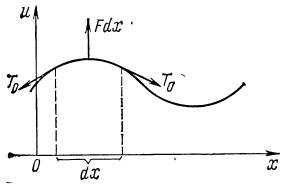
Ограничимся рассмотрением малых, поперечных и плоских коллебаний струны, т.е. таких коллебаний, при которых отклонения точек струны от положения покоя малы, в любой момент времени все точки стуны находятся в одной и тойже плоскости и каждая точка струны колеблется, оставаясь на одном и там же перпендикуляре к прямой, соответствующей состоянию покоя струны.

Принимая эту прямую за ось \(Ox\), обозначим через \(u=u(x,t)\) отклонение точек струны от положения равновесия в момент времени \(t\). При каждом фиксированом значении \(t\) график функции \(u=u(x,t)\) на плоскости \(xOu\) дает форму стуны в момент времени \(t\).

Пример 1. Найти решение уравнения

$$\frac{\partial ^2u}{\partial t^2}=\frac{\partial ^2u}{\partial x^2}$$

если \(u\mid _{t=0}=x^2,\frac{\partial u}{\partial t}\mid _{t=0}=0.\)

Так как \(a=1\), а \(\psi (x)=0\), то

$$u=\frac{\varphi (x-at)+}\varphi (x+at){2}$$

где \(\varphi (x)=x^2\)

Таким образом,

\(u=\frac{(x-t)^2+(x+t)^2}{2}\) или \(u=x^2+t^2.\)

Пример 2. Найти решение уравнения

$$\frac{\partial ^2u}{\partial t^2}=4\frac{\partial ^2u}{\partial x^2}$$

если \(u\mid _{t=0}=0,\frac{\partial u}{\partial t}\mid _{t=0}=x.\)

Здесь \(a=2,\varphi (x)=0,\psi (x)=x.\) Отсюда

$$u=\frac{1}{4}\int_{x-2t}^{x+2t}{zdz}=\frac{1}{8}z^2\mid ^{x+2t}_{x-2t}=\frac{1}{8}[(x+2t)^2-(x-2t)^2]$$

т.е. \(u=xt.\)

Пример 3. Найти форму стурны, определяемой уравнением

$$\frac{\partial ^2u}{\partial t^2}=a^2\frac{\partial ^u}{\partial x^2}$$

в момент \(t=\frac{\pi }{2a}\), если \(u\mid _{t=0}=\sin x, \frac{\partial u}{\partial t}\mid _{t=0}=1.\)

Имеем

$$u=\frac{\sin (x+at)+\sin (x-at)}{2}+\frac{1}{2a}\int_{x-at}^{x+at}{dz},$$

$$u=\sin x\cos at+\frac{1}{2a}z\mid _{x-at}^{x+at}$$

или

$$u=\sin x\cos at+t.$$

Если \(t=\pi /(2a)\) , то \(u=\pi /(2a)\) ,т.е. струна паралельна оси абсцисс.

Пример 1. Дана струна, закрепленная на концах \(x=0, x=l\). Пусть в начальный момент форма струны имеет вид ломаной (OAB,\) изображонной на рисунке.

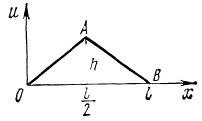
Угловой коэффициент прямой \(OA\) равен \(h/(l/2)\) т.е. \(2h/l\).

Следовательно уравнение этой прямой есть \(u=(2h/l)\). Прямая \(AB\) отсекает на осях координат отрезки \(l\) и \(2h\); значит, уравнение этой прямой имеет вид \(x/l+u/(2h)=1,\) или \(u=(2h/l)(l-x).\) Итак,

$$\varphi (x)=\begin{cases} & \text{ } (2h/l)x ;0\leq x\leq l/2, \\ & \text{ } (2h/l)(l-x) ;l/2\leq x\leq l,\psi (x)=0. \end{cases}$$

Находим

$$a_k=\frac{2}{l}\int_{0}^{l}{\varphi (x)\cdot \sin \frac{k\pi x}{l}dx}=\frac{4h}{l^2}\int_{0}^{l/2}{x\sin \frac{k\pi x}{l}dx}+\frac{4h}{l^2}\int_{l/2}^{l}{(l-x)\sin \frac{k\pi x}{l}dx},$$

Интегрируя по частям получаем

$$a_k=-\frac{4h}{k\pi l}\cdot x\cdot \cos \frac{k\pi x}{l}\mid _0^{l/2}+\frac{4h}{k\pi l}\int_{0}^{l/2}{\cos \frac{k\pi x}{l}dx}-$$

$$-\frac{4h}{k\pi l}(l-x)\cdot \cos \frac{k\pi x}{l}\mid _l/2^{l}-\frac{4h}{k\pi l}\int_{l/2}^{l}{\cos \frac{k\pi x}{l} dx}=$$

$$=-\frac{2h}{k\pi }\cdot \cos \frac{k\pi }{2}+\frac{4h}{k^2\pi ^2}\cdot \sin \frac{k\pi x}{l}\mid _0^{l/2}+\frac{2h}{k\pi }\cdot \cos \frac{k\pi }{2}-\frac{4h}{k^2\pi ^2}\cdot \sin \frac{k\pi x}{l}\mid ^l_{l/2}=$$

$$=\frac{4h}{k^2\pi ^2}\cdot \sin \frac{k\pi }{2}+\frac{4h}{k^2\pi ^2}\cdot \sin \frac{k\pi }{2}=\frac{8h}{k^2\pi ^2}\cdot \sin \frac{k\pi }{2}.$$

Следовательно,

$$u(x,t)=\frac{8h}{\pi ^2}\cdot \sum_{k=1}^{\infty }{\frac{1}{k^2}}\cdot \sin \frac{k\pi }{2}\cdot \sin \frac{k\pi x}{l}\cdot \cos \frac{k\pi at}{l}.$$

2012-12-16 • Просмотров [ 20613 ]