Знайти площу частини сфери:
$$x^2+y^2+z^2=a^2,$$
що міститься всередині циліндра \(x^2+y^2=ay\;(x\geq 0,\;y\geq 0,z\geq 0).\)
Розв'язання:
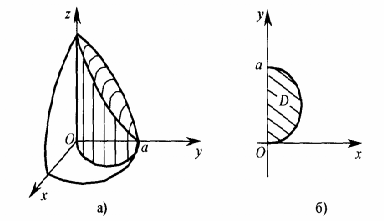
Частина сфери, що знаходиться в першому октанті і міститься всередині циліндра, проектується у півкруг, обмежений колом \(x^2+y^2=ay\) та віссю Оу (рис.1).
З рівняння сфери маємо:
$$z=\sqrt{a^2-x^2-y^2};\;\frac{\partial z}{\partial x}=-\frac{x}{\sqrt{a^2-x^2-y^2}};\;\frac{\partial z}{\partial y}=-\frac{y}{\sqrt{a^2-x^2-y^2}};$$
$$\sqrt{1+z'^2_x+z'^2_y}=\sqrt{1+\frac{x^2}{a^2-x^2-y^2}+\frac{y^2}{a^2-x^2-y^2}}=\frac{a}{a^2-x^2-y^2}$$
Отже,
$$S={\int \int}_{D} \frac{a}{\sqrt{a^2-x^2-y^2}}dxdy.$$
Перейдемо до полярних координат. Врахуємо, що рівняння кола прийме вигляд \(\rho=a \sin \varphi\).
$$S=a{\int \int}_{D} \frac{dxdy}{\sqrt{a^2-x^2-y^2}}=\left|\matrix{x=\rho\cos \varphi,& D\rightarrow D',\\ y=\rho\sin \varphi,& D':0\leq\rho\leq a\sin \varphi ,\\dxdy=\rho d \rho d \varphi,&0\leq \varphi\leq \frac{\pi}{2}.}\right|=$$
$$=a{\int \int}_{D} \frac{\rho d \rho d \varphi}{\sqrt{a^2-\rho^2}}=a\int_{0}^{\pi/2}{d \varphi}\int_{0}^{a \sin \varphi}{\frac{\rho d \rho}{\sqrt{a^2-\rho^2}}}=$$
$$=-a\int_{0}^{\pi/2}\left(\sqrt{a^2-\rho^2}\mid _{0}^{a \sin \varphi} \right) d \varphi=-a^2\int_{0}^{\pi/2}(\cos \varphi-1)d \varphi=$$
$$=-a^2 (\sin \varphi-\varphi)\mid_{0}^{\pi/2}=-a^2 \left(1-\frac{\pi}{2} \right)=a^2\left(\frac{\pi}{2}-1 \right).$$