Предикаты, так же, как высказывания, могут принимать два значения: "истина" и "ложь", поэтому к ним применимы все операции логики высказываний, в результате чего из элементарных предикатов формируются сложные предикаты (как и в логике высказываний, где из элементарных высказываний формировались сложные, составные).
    Рассмотрим применение операций логики высказываний к предикатам на примерах одноместных предикатов. Эти операции в логике предикатов сохраняют тот же смысл, который был им присвоен в логике высказываний.
    Пусть на некотором множестве \(M\) определены два предиката \(P ( x)\) и \(Q ( x)\).
    Конъюнкцией двух предикатов \(P ( x)\) и \(Q ( x)\) называется новый предикат \(P (x) \wedge Q ( x)\), который принимает значение "истина" при тех и только тех значениях \(x \epsilon M\), при которых каждый из предикатов принимает значение "истина", и принимает значение "ложь" во всех остальных случаях.
    Очевидно, что областью истинности предиката \(P (x) \wedge Q ( x)\) является общая часть области истинности предикатов \(P ( x)\) и \(Q ( x)\), то есть пересечение \(I_{P} \bigcap{} I _{Q}\).
    Так, например, для предикатов \(P (x):\) "\(x\) – четное число" и \(Q ( x)\): "\(x\) кратно 3" конъюнкцией \(P (x) \wedge Q ( x)\) является предикат "\(x\) – четное число и \(x\) кратно 3", то есть предикат "\(x\) делится на 6".
    Дизъюнкцией двух предикатов \(P ( x)\) и \(Q ( x)\) называется новый предикат \(P (x) \vee Q ( x)\), который принимает значение "ложь" при тех и только тех значениях \(x \epsilon M\), при которых каждый из предикатов принимает значение "истина", и принимает значение "ложь" во всех остальных случаях.
    Ясно, что областью истинности предиката \(P (x) \vee Q ( x)\) является объединение области истинности предикатов \(P ( x)\) и \(Q ( x)\), то есть объединение \(I_{P } \bigcup{} I_{Q}\).
    Отрицанием предиката \(P (x)\) называется новый предикат \(\bar{P}(x)\), который принимает значение "истина" при всех значениях \(x \epsilon M\), при которых предикат \(P (x)\) принимает значение "ложь", и принимает значение "ложь" при тех значениях \(x \epsilon M\), при которых предикат \(P (x)\) принимает значение "истина".
    Из этого определения следует, что \(I _{\bar{P}} = M\) \ \(I _{P} = C I _{P}\).
    Импликацией предикатов \(P (x)\) и \(Q (x)\) называется новый предикат \(P (x) \rightarrow Q (x)\), который является ложным при тех и только тех значениях \(x \epsilon M\), при которых одновременно \(P (x)\) принимает значение "истина", \(Q (x)\) – значение "ложь", и принимает значение "истина" во всех остальных случаях.
    Так как при каждом фиксированном \(x \epsilon M\) справедлива равносильность \(P (x) \rightarrow Q ( x) \equiv \bar{P} (x) \vee Q (x)\), то \(I _{P\rightarrow Q} = I _{\bar{P}} \bigcup{} I_{Q} = CI_{P} \bigcup{} I _{Q}\).
    Эквиваленцией предикатов \(P (x)\) и \(Q (x)\) называется новый предикат \(P (x) \leftrightarrow Q (x)\), который обращается в "истину" при всех тех и только тех \(x \epsilon M\), при которых \(P (x)\) и \(Q (x)\) обращаются оба в истинные или оба в ложные высказывания.
    Для его множества истинности имеем: \(I _{P\leftrightarrow Q} = I_{\bar{P}} \bigcap{} I _{\bar{Q}} \bigcup{} I _{P} \bigcap{} I _{Q}\).
    Пример 1. Пусть даны предикаты: \(P ( x)\): "\(x\) - четное число" и \(Q (x )\): "\(x\) кратно 3", определенные на множестве \(N\). Найти области истинности предикатов:
    1) \(P ( x) \wedge Q (x)\);
    2) \(P ( x) \vee Q (x)\);
    3) \(\bar{P} ( x)\);
    4) \(P ( x) \rightarrow Q (x)\).
    Решение. Так как \(I_{P} =\)\(\begin{Bmatrix} 2, 4, 6, ..., 2n, ... \end{Bmatrix}\), \(I_{Q} =\)\(\begin{Bmatrix} 3, 6, 9, ..., 3n, ... \end{Bmatrix}\), то
    1) \(I _{P \wedge Q} = I_{P} \bigcap{} I _{Q} = \begin{Bmatrix} 6, 12, ... , 6n, ... \end{Bmatrix}\);
    2) \(I _{P \vee Q} = I_{P} \bigcup{} I _{Q} = \begin{Bmatrix} 2, 3, 4, 6, ..., 2n, 3n,... \end{Bmatrix}\);
    3) \(I _{\bar{P}} = CI_{P}= N\)\ \(I _{P} = \begin{Bmatrix} 1, 3, 5, ..., 2n -1, ... \end{Bmatrix}\);
    4) \(I _{P \rightarrow Q} = C I _{P} \bigcup{} I _{Q} = \begin{Bmatrix} 1,3,5,...,2n-1,... \end{Bmatrix} \bigcup{} \begin{Bmatrix} 3, 6, 9, ..., 3n, ... \end{Bmatrix}\).
    Сказанное позволяет находить области истинности более сложных предикатов, полученных в результате применения к исходным предикатам логических операций.
    Пример 2. Пусть даны предикаты \(A ( x, y)\) и \(B ( x, y)\), определенные на множестве \(M = M_{1} \times M _{2} \subset R \times R\). Найти множество истинности предиката \(A ( x, y) \leftrightarrow B ( x,y)\) и изобразить ее с помощью KpyroB Эйлера-Венна.
    Так как \(A ( x, y) \leftrightarrow B ( x,y) = (A ( x,y) \rightarrow B ( x,y)) \wedge ( B ( x,y) \rightarrow A ( x,y))\), то $$I _{A\leftrightarrow B} = ( I _{A\rightarrow B}) \bigcap{} (I _{B \rightarrow A}) = ((CI_{A} \bigcup{} I_{B}) \bigcap{} ( CI_{B} \bigcup{} I _{A})) =$$ ( I _{A} \bigcap{ } I_{B}) \bigcup{} ( CI_{A} \bigcap{} CI_{B}).
    \(I _{A} \leftrightarrow I_{B}\) изображена заштрихованной частью рисунка:

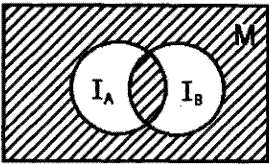
    Можно рассматривать и обратную задачу: Зная область истинности предиката, полученного в результате применения логических операций к некоторым предикатам, записать этот предикат.
    Пример 3. Записать предикат, полученный в результате логических операций над предикатами \(P (x) , Q ( x)\) n \(R (x)\) область истинности которого \(I\) заштрихована на рисунке.
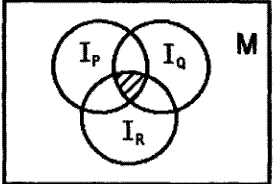
    Так как здесь \(I = I_{P} \bigcap{} I _{Q} \bigcap{} I _{R}\), то искомый предикат имеет вид \(P ( x) \wedge Q (x) \wedge R (x)\).

---