В тестовых заданиях на ЕГЭ или ЗНО, как правило всегда присутствуют задания вычислительного характера, имеющие отношение к геометрическим фигурам. Причина этого очевидна - результатом таких задач должно быть число, а значит легко проверить правильность результата, если тестирование и проверка проводится автоматически. Приведем некоторые типичные примеры задач на вычисления.
Если задачи, в которых фигурирует прямоугольник или квадрат относят к числу простейших, то задачи с параллелограммом уже несколько сложнее. Как ни странно, но формулу вычисления площади параллелограмма знают не все. А учитывая, что имеется множество достаточно хитрых свойств у параллелограмма, то придумать можно огромное число разнообразных задач. Больше про параллелограмм и его свойства тут: https://microexcel.ru/parallelogramm/. Приведем дальше несколько примеров вычислительных задач с использованием нашего онлайн математического блокнота, в который вы можете носить ваши данные и прямо тут проводить свои собственные вычисления.
Задача. Типичной считается задача на вычисление площади параллелограмма. Заданы длина основания параллелограмма \(a=4\) и высота параллелограмма \(h=3\) . Обозначения основания и высоты приведены на рисунке. Площадь параллелограмма вычисляется как произведение длины основания на высоту по формуле: \(S=a \cdot h\). Запишем эту формулу в наш блокнот, в котором вы сможете менять значения основания и высоты на свои.
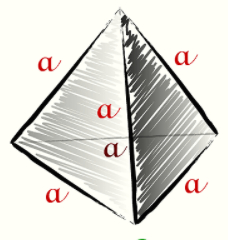Ну и конечно же излюбленным 3D-обьектом тут есть тетраэдр, с его свойствами и формулами для вычисления площади поверхности и объема. Если вы забыли что такое тетраэдр, то вспоминайте тут: https://microexcel.ru/tetraedr/. Приведем снова наш математический блокнот с типичной задачей для тетраэдра.
Задача. Пусть задан тетраэдр с длиной ребра, равной \(a=4\). Как известно, объем такого тетраэдра вычисляется по формeле: \(V=a^3 \cdot \sqrt(2)/12\). Чтобы подставить ваши значения поставьте курсор на строку \(a=4\) и она станет доступной для редактирования.
