Преобразование Фурье — операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами. Обратное преобразование Фурье означает просто то, что нам необходимо сложить все соответствующие составляющие частоты в каждый момент времени.
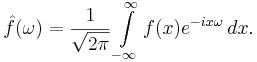
Смысл преобразования Фурье
Преобразование Фурье переводит функцию из временной или пространственной области в частотную. Это позволяет определить, из каких гармонических компонент состоит сигнал, оценить их амплитуды и фазы.
Преобразование Фурье для элементарных функций
Экспоненциальная функция
Задача: найти преобразование Фурье функции \( f(t)=e^{-a t}\cdot u(t) \), где \(u(t)\) — функция Хевисайда.
Команда для калькулятора:
FourierTransform[Exp[-a t] HeavisideTheta[t], t, ω]
Результатом будет рациональная функция от \(\omega\), показывающая спектральное распределение экспоненциального затухания.
Гармоническая функция
Задача: вычислить преобразование Фурье функции \( f(t)=\sin(\omega_0 t) \).
Команда для калькулятора:
FourierTransform[Sin[ω0 t], t, ω]
Спектр такой функции состоит из двух дельта-пиков, что отражает наличие одной частоты.
Преобразование Фурье для полиномиальных и составных функций
Полиномиально-экспоненциальная функция
Задача: найти спектр функции \( f(t)=t e^{-t^2} \).
Команда для калькулятора:
FourierTransform[t Exp[-t^2], t, ω]
Подобные примеры часто используются при анализе оконных функций и сглаживания сигналов.
Функция с ограниченной областью определения
Задача: вычислить преобразование Фурье функции \( f(t)=1 \) на интервале \([-1,1]\).
Команда для калькулятора:
FourierTransform[Boole[-1 <= t <= 1], t, ω]
В результате получается выражение типа \(\mathrm{sinc}\), характерное для прямоугольных импульсов.
Дискретное преобразование Фурье
Для числовых данных используется дискретное преобразование Фурье, которое лежит в основе спектрального анализа временных рядов.
Последовательность чисел
Задача: выполнить дискретное преобразование Фурье для набора значений \(\{1,2,1,0\}\).
Команда для калькулятора:
Fourier[{1, 2, 1, 0}]
Результат позволяет определить вклад различных гармоник в дискретном сигнале.
Обратное преобразование Фурье
Обратное преобразование Фурье используется для восстановления исходной функции по известному спектру:
\[ f(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty} F(\omega)\,e^{i\omega t}\,d\omega \]
Восстановление функции из спектра
Задача: найти обратное преобразование для функции \( F(\omega)=\frac{1}{1+\omega^2} \).
Команда для калькулятора:
InverseFourierTransform[1/(1 + ω^2), ω, t]
Подобные вычисления применяются при решении дифференциальных уравнений и задач фильтрации.
Интересный факт о преобразовании Фурье
Преобразование Фурье применяется не только в математике и физике, но и в сжатии изображений, например в формате JPEG.
Онлайн калькулятор
Важно. Вставить в калькулятор код можна нажав на значок копирования в строке с кодом примера или набрав код вручную. Можно воспользоваться справочником примеров команд для калькулятора: примеры для онлайн калькулятора. Потом нажать кнопку "Решить". Если на узком экране смартфона кнопка калькулятора не нажимается, поверните экран горизонтально.