Задачу, в которой по данным, полученным в результате эксперимента или измерений, приходится решать студентам и специалистам в разных областях деятельности. Например, при решении экономических задач или задач прогнозирования. Чаще всего требуется решить задачу линейно регрессии или построить квадратичную или кубическую линию регрессии. Иногда - экспоненциальную регрессию. Тип регрессии зависит от исходного набора данных.

Итак, в задаче как правило задан набор пар данных. Требуется построить кривую, наилучшим образом описывающую эти данные. А также найти уравнение этой кривой. С помощью нашего решателя это можно сделать быстро и просто. Для этого надо ввести в решатель соответствующую команду. Приведем пример команды для линейной регрессии. 

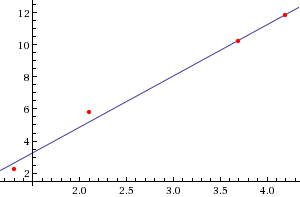
linear fit {1.3, 2.2},{2.1, 5.8},{3.7, 10.2},{4.2, 11.8}
В результате будет получен график, который вы видите на картинке вверху слева и уравнение прямой регрессии: \(3.19383 x-1.52256\). Красные точки на рисунке - точки построенные по исходным данным, а прямая линия - искомая линия регрессия.

Теперь приведем пример команды для квадратичной регрессии: 
quadratic fit {10.1,1.2},{12.6, 2.8},{14.8,7.6},{16.0,12.8},{17.5,15.1}
Для кубической регрессии команда имеет вид, приведенный ниже. Обратите внимание на этот пример. Здесь введены только данные второй координаты. Если первая не вводится (как в этом примере), то по умолчанию в качестве первой координаты берутся порядковые номера данных из набора данных. 
cubic fit 20.9,23.2,26.2,26.4,16.3,-12.2,-60.6,-128.9
И еще один пример - экспоненциальная регрессия: 
exponential fit 0.783,0.552,0.383,0.245,0.165,0.097
А теперь логарифмическая регрессия: 
log fit {15.2,8.9},{31.1,9.9},{38.6,10.3},{52.2,10.7},{75.4,11.4}
Чтобы попробовать решатель в работе, скопируйте любой пример (ctrl+c) и вставьте в решатель (ctrl+v), а потом нажмите кнопку "решить".

Оценка - 4.8 (18)
 Похожие публикации
2015-11-22 • Просмотров [ 13419 ]