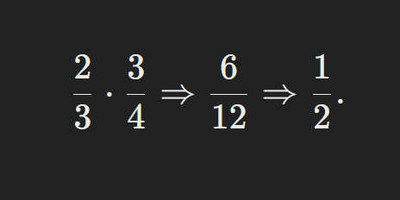Обчислення з дробами є важливою частиною математики, але часто викликають труднощі, особливо для тих, хто тільки починає працювати з ними. У цій статті ми розглянемо, чому обчислення з дробами можуть бути складними, наведемо причини типових помилок, а також покажемо приклади неправильних і правильних рішень.
Чому дроби викликають складності?
- Робота з різними знаменниками: Щоб додавати чи віднімати дроби, їх потрібно приводити до спільного знаменника.
- Перетворення дробів: Потрібно вміти перетворювати неправильні дроби в мішані числа і навпаки.
- Правила множення та ділення: Ці операції часто плутають із додаванням та відніманням.
- Скорочення дробів: Неправильне скорочення може призвести до помилкових результатів.
Типові помилки та їх виправлення
1. Неправильне додавання дробів з різними знаменниками
Помилка:
$$\frac{1}{2} + \frac{1}{3} ⇒ \frac{2}{5}.$$
Правильно:
$$\frac{1}{2} + \frac{1}{3} ⇒ \frac{3}{6} + \frac{2}{6} ⇒ \frac{5}{6}.$$
2. Помилка при відніманні дробів
Помилка:
$$\frac{3}{4} - \frac{1}{2} ⇒ \frac{2}{2} ⇒ 1.$$
Правильно:
$$\frac{3}{4} - \frac{1}{2} ⇒ \frac{3}{4} - \frac{2}{4} ⇒ \frac{1}{4}.$$
3. Неправильне множення дробів
Помилка:
$$\frac{2}{3} \cdot \frac{3}{4} ⇒ \frac{6}{7}.$$
Правильно:
$$\frac{2}{3} \cdot \frac{3}{4} ⇒ \frac{6}{12} ⇒ \frac{1}{2}.$$
4. Неправильне ділення дробів
Помилка:
$$\frac{2}{3} ÷ \frac{3}{4} ⇒ \frac{6}{12}.$$
Правильно:
$$\frac{2}{3} ÷ \frac{3}{4} ⇒ \frac{2}{3} \cdot \frac{4}{3} ⇒ \frac{8}{9}.$$
5. Неправильне скорочення дробів
Помилка:
$$\frac{8}{12} ⇒ \frac{4}{6} ⇒ 3.$$
Правильно:
$$\frac{8}{12} ⇒ \frac{2}{3}.$$
6. Помилки при роботі з мішаними числами
Помилка:
$$2 \frac{1}{3} + 1 \frac{2}{3} ⇒ 3 \frac{3}{6}.$$
Правильно:
$$2 \frac{1}{3} + 1 \frac{2}{3} ⇒ \frac{7}{3} + \frac{5}{3} ⇒ \frac{12}{3} ⇒ 4.$$
Як уникати помилок?
- Завжди приводьте дроби до спільного знаменника при додаванні чи відніманні.
- Перевіряйте правильність виконання операцій: Не плутайте множення з діленням.
- Скорочуйте дроби до найпростішого вигляду, використовуючи найбільший спільний дільник.
- Розвивайте уважність: Перевіряйте кожен крок обчислень, щоб уникнути механічних помилок.
Обчислення з дробами можуть бути складними, але дотримання правил і уважність допоможуть уникнути помилок. Практика і перевірка кожного кроку — ключ до успішного розв'язання задач із дробами.
Схожі публікації