Числа расположены следующим образом:

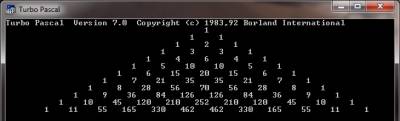
Первый и последний члены в каждой строке равны 1, а каждый из прочих членов равен сумме двух ближайших находящихся сверху чисел. Такое расположение чисел называется треугольником Паскаля, хотя до Б. Паскаля (Pascal, 1623-1662) оно было известно итальянскому математику Н. Тарталье (Tartaglia, 1500-1557), а еще раньше этот треугольник был описан в работах арабских математиков.

Program TreugPas;
uses crt;
const n=12; {число строк треугольника Паскаля}
type treug=array [1..n] of array [1..n] of integer;
var tt: treug;
procedure Pascal (var t:treug);
 var i, j: 1..n;
begin
 for i:=1 to n do
 for j:=i+1 to n do
 t[i, j]:=0;
 for i:=1 to n do
 t[i, 1]:=1;
 for i:=2 to n do
 for j:=2 to i do
 t[i, j]:=t[i-1, j-1]+t[i-1, j]
end;
procedure pechat (t:treug); {процедура печати}
var i, j, s: 1..n;
function chcf (n:integer):integer;
{число цифр}
var k:integer;
begin
 k:=0;
 repeat
 k:=k+1;
 n:=n div 10
 until n=0;
 chcf:=k
end;
begin
s:=chcf(t[n, n div 2+1]); {самое большое число цифр}
for i:=1 to n do
 begin
 write(' ':(n-i+1)*s); {пробелы в начале строки}
 for j:=1 to i do
 write(t[i, j]: 2*s);
 writeln
 end
end;
begin
Pascal(tt);
pechat(tt);
readkey
end.

Поскольку в треугольнике Паскаля должны быть оставлены пробелы между числами, то для печати каждой строки мы выделяем вдвое больше позиций, нежели занимает самое длинное число (число, в котором больше всего цифр). Его длина устанавливается функцией chcf.

---