Рассмотрим подход к получению функции трудоемкости рекурсивного алгоритма, основанный на непосредственном подсчете вершин дерева рекурсивных вызовов, на примере алгоритма сортировки слиянием.

Рекурсивная процедура Merge Sort – MS получает на вход массив А и два индекса p и q, указывающие на ту часть массива, которая будет сортироваться при данном вызове. Вспомогательные массивы Bp и Bq используются для слияния отсортированных частей массива.

MS(A, p ,q, Bp, Bq)
If p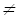q (проверка останов рекурсии при p=q)
then
r<--(p+q) div 2
MS(A, p, r, Bp,Bq) (рекурсивный вызов для первой части)
MS(A, r+1, q, Bp,Bq) (рекурсивный вызов для второй части)
Merge(A, p, r, q, Bp, Bq) (слияние отсортированных частей)
Return (A)
End

2. Слияние отсортированных частей (Merge)

Рассмотрим процедуру слияния отсортированных частей массива А, использующую дополнительные массивы Bp и Bq, в конец которых с целью остановки движения индекса помещается максимальное значение. Поскольку сам алгоритм рекурсивной сортировки устроен так, что объединяемые части массива А находятся рядом друг с другом, то алгоритм слияния вначале копирует отсортированные части в промежуточные массивы, а затем формирует объединенный массив непосредственно в массиве А.

Merge (A,p,r,q,Bp,Bq) (В {} взято количество операций в данной строке)

Max <-- A[r] {2}
If Max Max <-- A[q] {(1/2)*2}
kp <-- r - p + 1 {3}
p1 <-- p – 1 {2}
For i <-- 1 to kp (копирование первой части) {1+kp*3}
Bp [ i ] <-- A[p1 + i ] {kp*(4)}
Bp[ kp+1] <-- Max {3}
kq <-- q - r {2}
For i <-- 1 to kq (копирование второй части) {1+ kq*3}
Bq [ i ] <-- A[ r + i ] {kq*(4)}
Bq [ kq+ 1] <-- Max {3}
(заметим, что m=kp + kq = q – p + 1 – длина объединенного массива)
pp <-- p {1}
pq <-- r+1 {2}
For i <-- p to q (слияние частей) {1+m*3}
If Bp [ pp ] < Bq [ pq ] {m*3}
Then
A[ i ] <-- Bp[ pp ] {(1/2)*m*3}
pp <-- pp +1 {(1/2)*m*2}
Else
A [ i ] <-- Bq [ pq ] {(1/2)*m*3}
pq <-- pq +1 {(1/2)*m*2}
Return(A)
End

На основании указанного количества операций можно получить трудоемкость процедуры слияния отсортированных массивов в среднем:

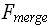(m) = 2+2+1+3+2+1+kp*7+3+2+1+kq*7+3+1+2+1+m*(3+3+3+2) = 11*m + 7*(kp+kq) + 23 = 18*m+23. (10.1)

3. Подсчет вершин в дереве рекурсивных вызовов

Алгоритм, получая на входе массив из n элементов, делит его пополам при первом вызове, поэтому рассмотрим случай, когда n=2^k, k =log₂n

Рис. Фрагмент рекурсивного дерева при сортировке слиянием

Обозначим количество вершин дерева через V:
V = n + n/2+n/4+n/8+...+1 = n*(1+1/2+1/4+1/8+...+1)=2n - 1= 2^k+1- 1

Из них все внутренние вершины порождают рекурсию, количество таких вершин – Vr = n-1, остальные n вершин – это вершины в которых рассматривается только один элемент массива, что приводит к останову рекурсии.