Задача. Дано целое число S. Требуется получить и вывести на экран все возможные различные способы представления этого числа в виде суммы натуральных чисел (то есть, 1 + 2 и 2 + 1 – это одинаковый способ разложения числа 3).
Решение.
Самое сложное в этой задаче – сразу исключить из рассмотрения повторяющиеся последовательности. Для этого будем рассматривать только невозрастающие последовательности слагаемых (каждое следующее слагаемое не больше предыдущего). Все слагаемые будем записывать в массив. Для этого нам понадобится массив (назовем его A) из S элементов, поскольку самое длинное представление - это сумма S единиц. Чтобы не расходовать память зря, лучше выделять его динамически (см. раздел про массивы). Пусть q элементов массива (с номерами от 0 до q-1) уже стоят на своих местах, причем A[q-1]=m. Каким может быть следующее слагаемое - элемент A[q]? Поскольку последовательность невозрастающая, он не может быть больше q. С другой стороны, он должен быть не больше, чем S-S0, где S0 - сумма предыдущих элементов. Очевидно, что минимальное значение этого элемента - единица. Эти размышления приводят к следующей процедуре, которая принимает в параметрах сумму оставшейся части, массив для записи результата и количество уже определенных элементов последовательности.
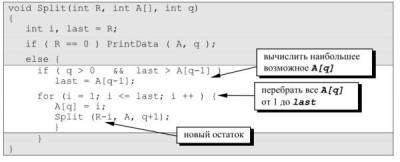
void Split(int R, int A[], int q)
{
int i, last = R;
if ( R == 0 ) PrintData ( A, q );
else {
if ( q > 0 && last > A[q-1] )
last = A[q-1];
for (i = 1; i <= last; i ++ ) {
A[q] = i;
Split (R-i, A, q+1);
}
}
}
Основная программа вызывает эту процедуру так (используется динамический массив):
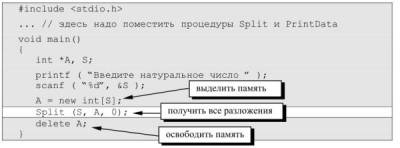
#include <stdio.h>
... // здесь надо поместить процедуры Split и PrintData
void main()
{
int *A, S;
printf ( "Введите натуральное число ” );
scanf ( "%d”, &S );
A = new int[S];
Split (S, A, 0);
delete A;
}