Пример 1. Вычислить \(\int \int _{D}x\ln ydx dy,\) если область \(D\) - прямоугольник \(0\leq x\leq 4,1\leq y\leq e\).

$$\int \int _{D}x\ln ydx dy=\int_{0}^{4}{xdx}\int_{1}^{e}{\ln ydy}=\left[\frac{x^2}{2} \right]_0^4\cdot [y\ln y-y]_1^e=8(e-e+1)=8.$$

Пример 2. Вычислить \(\int \int _{D}(\cos ^2x+\sin ^2y)dxdy,\) если область \(D\) - квадрат \(0\leq x\leq \pi /4,0\leq y\leq \pi /4.\)

$$\int \int _{D}(\cos ^2x+\sin ^2y)dxdy=\int_{0}^{\pi /4}{dx}\int_{0}^{\pi /4}{\cos ^2x+\sin ^2y}dy=$$

$$=\int_{0}^{\pi /4}{[y\cos ^2x+\frac{y}{2}-\frac{1}{4}\sin 2y]_0^{\pi /4}dx}=\int_{0}^{\pi /4}(\frac{\pi }{4}\cos ^2x+\frac{\pi }{8}-\frac{1}{4})dx=$$

$$=[\frac{\pi }{8}(x+\frac{1}{2}\sin 2x)+(\frac{\pi }{8}-\frac{1}{4})x]_0^{\pi /4}=\frac{\pi }{8}(\frac{\pi }{4}+\frac{1}{2})+(\frac{\pi }{8}+\frac{1}{4})\frac{\pi }{4}=\frac{\pi ^2}{16}.$$

Пример 3. Вычислить \(\int \int _{D}(x-y)dxdy\) , если область \(D\) ограничена линиями \(y=2-x^2,y=2x-1.\)

Построим область \(D\) . Первая линия - папабола с вершиной в точке \((0;2)\) , симметричная относительно оси \(Oy\). Вторая линия - прямая. Решая совсместно уравнения \(y=2-x^2,y=2x-1,\) найдем координаты точек пересичения: \(A(-3;-7),B(1;1)\)

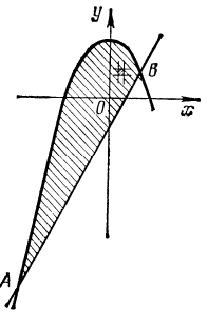
Область интегрирования принадлежит к первому виду. Находим

$$\int \int _{D}(x-y)dxdy=\int_{-3}^{1}{dx}\int_{2x-1}^{2-x^2}{(x-y)dy}=\int_{-3}^{1}{[xy-\frac{1}{2}y^2]_{2x-1}^{2-x^2}dx}=$$

$$=\int_{-3}^{1}{(2x-x^3-2+2x^2-\frac{1}{2}x^4-2x^2+x+2x^2-2x+\frac{1}{2})dx}=\int_{-3}^{1}{(-\frac{1}{2}x^4-x^3+2x^2+x-\frac{3}{2})dx}=$$

$$=[-\frac{1}{10x^5}-\frac{1}{4}x^4+\frac{2}{3}x^3+\frac{1}{2}x^2-\frac{3}{2}x]_{-3}^1=4\frac{4}{15.}$$

Пример 4. Вычислить \(\int \int _{D}(x+2y)dxdy,\) если область \(D\) ограничена приямыми \(y=x,y=2x,x=2,x=3.\)

$$\int \int _{D}(x+2y)dxdy=\int_{2}^{3}{dx}\int_{x}^{2x}{(x+2y)dy}=\int_{2}^{3}{[xy+y^2]_x^{2x}dx}=$$

$$=\int_{2}^{3}{(2x^2+4x^2-x^2-x^2)dx}=4\int_{2}^{3}{x^2dx}=\frac{4}{3}x^3\mid ^3_2=25\frac{1}{3}.$$

Преобразование двойного интеграла от прямоугольных координат \(x,y\) к полярным координатам \(\rho ,\theta\), связанным с прямоуголбными координатами соотношениями \(x=\rho \cos \theta ,y=\rho \sin \theta ,\) осуществляется по формуле

$$\int \int _{D}f(x,y)dxdy=\int \int _{D}f(\rho \cos \theta ,\rho \sin \theta)\rho d\rho d\theta .$$

Пример 1. Перейдя к полярным координатам, вычислить двойной интеграл \(\int \int _{D}\sqrt {x^2+y^2}dxdy\),если \(D\) - І четверть круга \(x^2+y^2\leq a^2.\)

Полагая \(x=\rho \cos \theta ,y=\rho \sin \theta \) имеем

$$\int \int _{D}\sqrt {x^2+y^2}dxdy=\int \int _{D}\sqrt {\rho ^2\cos ^2\theta +\rho ^2\sin ^2\theta }\rho d\rho d\theta =$$

$$=\int_{0}^{\pi /2}{d\theta }\int_{0}^{a}{\rho ^2d\rho }=\frac{1}{3}\int_{0}^{\pi /2}{\rho ^3}\mid _0^ad\theta =\frac{a^3}{3}\int_{0}^{\pi /2}{d\theta }=\frac{\pi a^3}{6}.$$

Пример 2. Вычислить \(\int \int _{D}\frac{x^2\sin (xy/2)}{y}dxdy,\) если область\(D\) ограничена четырьма параболами \(x^2=\pi y/3,x^2=2\pi y/3,y^2=2x,y^2=4x.\)

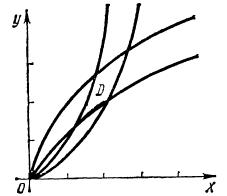
Произведем замену переменных так, чтобы \(xy=uv,x^2/y=v\); тогда \(x=\sqrt [3]{uv^2},y=\sqrt [3]{u^2v}\) и область \(D^{'}\) окажется прямоугольником \(u=2,u=4,v=\pi /3,v=2\pi /3.\)

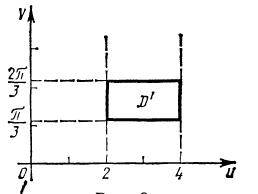
Находим якобиан преобразования:

$$J=\begin{vmatrix} \frac{1}{3}u^{-2/3}v^{2/3}&\frac{2}{3}u^{1/3}v^{-1/3} \\ \frac{2}{3}u^{-1/3}v^{1/3} & \frac{1}{3}u^{2/3}v^{-2/3} \end{vmatrix}=\frac{1}{9}-\frac{4}{9}=-\frac{1}{3}$$

т.е. \(\left|J \right|=\frac{1}{3}.\)

Следовательно,

$$\int \int _{D}\frac{x^2\sin (xy/2)}{y}dxdy=\frac{1}{3}\int \int _{D}\frac{u^{2/3}v^{4/3}\sin (uv/2)}{u^{2/3}v^{1/3}}dudv=$$

$$=\frac{1}{3}\int_{\pi /3}^{2\pi /3}{vdv}\int_{2}^{4}{\sin (uv/2)du}=\frac{2}{3}\int_{\pi /3}^{2\pi /3}(\cos v-\cos 2v)dv=$$

$$=\frac{2}{3}(\sin \frac{2\pi }{3}-\sin \frac{\pi}{3})-\frac{1}{3}(\sin \frac{4\pi }{3}-\sin \frac{2\pi}{3})=$$

$$=-\frac{1}{3}(-\frac{\sqrt 3}{2}-\frac{\sqrt 3}{2})=\frac{\sqrt 3}{2}=0,577.$$

2012-12-18 • Просмотров [ 6393 ]