Обчислити масу та середню густину пластинки D, яка обмежена лініями \(y=x^2,\;y=1,\) якщо густина визначається функцією \(\mu(x,y)=x^2+y^2.\)
Розв'язання:
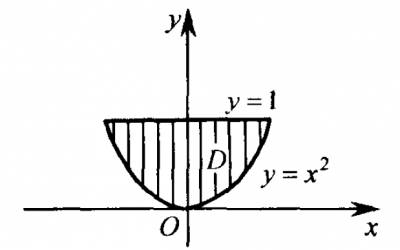
Пластинка D зображена на рис.1
Обчислимо масу пластинки D:
$$m={\int \int}_{D}\mu(x,y) dxdy={\int \int}_{D}(x^2+y^2) dxdy=\int_{-1}^{1}{dx}\int_{x^2}^{1}{(x^2+y^2) dy}=$$
$$=\int_{-1}^{1}\left(\left(x^2y+\frac{y^3}{3} \right)\mid _{x^2}^{1} \right){dx}=\int_{-1}^{1}\left(x^2-x^4+\frac{1}{3}-\frac{x^6}{3} \right)dx=$$
$$=\left(\frac{x^3}{3}-\frac{x^5}{5}+\frac{x}{3}-\frac{x^7}{21} \right)\mid _{-1}^{1}=\frac{44}{105}.$$
Знайдемо площину пластинки D, враховуючи симетрію пластинки відносно осі Oy:
$$S={\int \int}_{D} dxdy=2{\int \int}_{D'} dxdy=2\int_{0}^{1}{dx}\int_{x^2}^{1}{dy}=2\int_{0}^{1}\left(y\mid_{x^2}^{1} \right)dx=$$
$$=2\int_{0}^{1}(1-x^2)dx=2\left(x-\frac{x^3}{3} \right)\mid_{0}^{1}=2\left(1-\frac{1}{3} \right)=\frac{4}{3}.$$
Тепер обчислимо середню густину пластинки \(\mu_{ser}\) :
$$\mu_{ser}=\frac{m}{S}=\frac{44\cdot 3}{105\cdot 4}=\frac{11}{35}.$$