Обчислити потрійний інтеграл \({\int \int\int}_{G} z dxdydz,\)
де G - область, що обмежена сферою \(x^2+y^2+z^2=4\) та параболоїдом обертання \(x^2+y^2=3z\). Розв'язання:
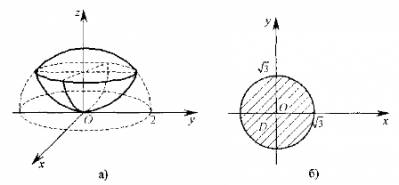
Рівняння \(x^2+y^2+z^2=4\) визначає сферу із центром у початку координат і радіусом \(R=4\), друга поверхня \(x^2+y^2=3z\) є параболоїд обертання навколо осі Oz . Побудуємо область G ( рис. а) та її проекцію D на площину хОу (рис. б).
Для визначення області D розв'яжемо систему рівнянь: $$\begin{cases}x^2+y^2+z^2=4, & \\ x^2+y^2=3z. & \end{cases}\ \Leftrightarrow \begin{cases}x^2+y^2=4-z^2, &\\ x^2+y^2=3z. & \end{cases}\Leftrightarrow \begin{cases}4-z^2=3z, &\\ x^2+y^2=3z. & \end{cases}\Leftrightarrow$$ $$\Leftrightarrow \begin{cases}z^2+3z-4=0, &\\ x^2+y^2=3z. & \end{cases}\ \Leftrightarrow \begin{cases}z_1=1, z_2=-4 &\\ x^2+y^2=3z. & \end{cases}\Leftrightarrow \begin{cases}z=1, &\\ x^2+y^2=3z. & \end{cases}$$
Маємо, що D є круг радіуса \(\sqrt{3}\), центр якого співпадає з початком координат, тобто \(D: x^2+y^2\leq 3\).
Перейдемо у потрійному інтегралі до циліндричних координат. Врахуємо, що у циліндричних координатах:
- рівняння сфери: \(\rho^2+z=4\) або \(z^2=4-\rho^2\);
- рівняння параболоїда обертання: \(\rho^2=3z\) або \(z=\frac{\rho^2}{3}\);
- рівняння кола \(\rho^2=3\).
Отже, \(G':0\leq \rho\leq \sqrt{3},\;0\leq \varphi\leq 2\pi,\;\frac{\rho^2}{3}\leq z\leq \sqrt{4-\rho^2}.\)
Таким чином: $${\int \int\int}_{G} z dxdydz=\left|\matrix{x=\rho\cos \varphi,& dxdydz=\rho d \rho d \varphi dz,\\ y=\rho\sin \varphi,& G\rightarrow G',\\z=z,}\right|=$$ $$={\int \int\int}_{G} z \rho d \rho d \varphi dz=\int_{0}^{2\pi}{d\varphi}\int_{0}^{\sqrt 3}{\rho d \rho}\int_{\frac{\rho^2}{3}}^{\sqrt {4-\rho^2}}{z dz}=$$ $$=\int_{0}^{2\pi}{d\varphi}\int_{0}^{\sqrt 3}{\rho}\left(\frac{z^2}{2}\mid _{\frac{\rho^2}{3}}^{\sqrt {4-\rho^2}} \right) d \rho=$$ $$=\frac{1}{2}\int_{0}^{2\pi}{d\varphi}\int_{0}^{\sqrt 3}{\rho} \left(4-\rho^2-\frac{\rho^4}{9} \right)d \rho=\frac{1}{2}\int_{0}^{2\pi}d \varphi \int_{0}^{\sqrt 3}\left(4\rho-\rho^3-\frac{\rho^5}{9} \right)d \rho=$$ $$=\frac{1}{2} 2\pi \left(\frac{4\rho^2}{2}-\frac{\rho^4}{4}-\frac{\rho^6}{54} \right)\mid _{0}^{\sqrt{3}}=\pi \left(6-\frac{9}{4}-\frac{27}{54} \right)=\frac{13}{4}\pi$$

---