Обчислити потрійний інтеграл \({\int \int\int}_{G} x dxdydz,\)
де G - тетраедр, що обмежений координатними площинами та площиною \(2x+2y+z-6=0.\)
Розв'язання:
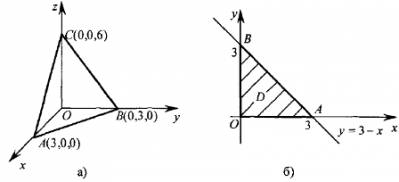
Тетраедр (рис. а) знизу обмежений площиною \(z= 0\), а зверху площиною \(z =6-2x-2y.\) Проекція D тетраедра на площину хОу є трикутник АОВ (рис. б), в якому у змінюється від \(y=0\) до \(y=3-x.\)

Таким чином, $${\int \int\int}_{G} x dxdydz={\int \int}_{D} dx dy\int_{0}^{6-2x-2y}{x}dz={\int \int}_{D} x dx dy\int_{0}^{6-2x-2y}dz=$$ $$={\int \int}_{D} \left(\int_{0}^{6-2x-2y}dz \right)x dx dy={\int \int}_{D} (6-2x-2y)xdx dy=$$ $$=\int_{0}^{3}{x}dx\int_{0}^{3-x}(6-2x-2y){dy}=\int_{0}^{3}\left( \int_{0}^{3-x}(6-2x-2y){dy}\right){x}dx=$$ $$=\int_{0}^{3}\left((6y-2xy-y^2)\mid _{0}^{3-x} \right){x}dx=\int_{0}^{3}(6(3-x)-2x(3-x)-(3-x)^2){xdx}=$$ $$=\int_{0}^{3}(18x-6x^2-6x^2+2x^3-9x+6x^2-x^3){dx}=\int_{0}^{3}(9x-6x^2+x^3){dx}=$$ $$=\left(\frac{9}{2}x^2-2x^3+\frac{x^4}{4}\mid_{0}^{3}\right)=\frac{81}{2}-54+\frac{81}{4}=\frac{243}{4}-54=\frac{27}{4}.$$

---