Знайти момент інерції рівнобедреного прямокутного трикутника відносно гіпотенузи довжини \(2а\), якщо в кожній точці його поверхнева густина пропорційна відстані точки до гіпотенузи.
Розв'язання:
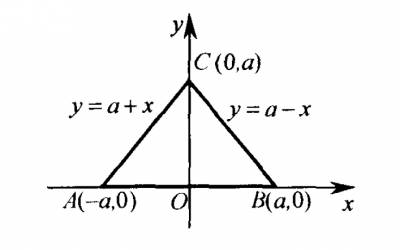
Нехай гіпотенуза заданого трикутника \(АВС\) розміщена на осі \(Ох\) і ділиться початком координат пополам (рис.1).


Рівняння катетів \(АС\) і \(СВ\) будуть відповідно \(y=a+x\) та \(y=a-x\), або \(x=y-a\) та \(x=a-y\). Густина \(\mu(х, у) = ky\) , де k - коефіцієнт пропорційності.
Шуканий момент інерції відносно гіпотенузи буде моментом інерції відносно осі \(Ох\), тобто \(I_х\). $$I_x={\int \int}_{D} y^2 \mu(x,y) dxdy={\int \int}_{D} ky^3 dxdy=k\int_{0}^{a}{y^3}dy\int_{y-a}^{a-y}{dx}=$$ $$=k\int_{0}^{a}{y^3}\left(x \mid_{y-a}^{a-y}\right)dy=k\int_{0}^{a}{y^3}(a-y-y+a)dy=$$ $$=2k\int_{0}^{a}{y^3}(a-y)dy=2k\left( a\frac{y^4}{4}-\frac{y^5}{5}\right)\mid_{0}^{a}=2k\frac{a^5}{20}=\frac{ka^5}{10}.$$

---