Задание 1. Действия с рациональными числами.
$$Вычислить \frac{1}{3}5,8+\frac{1}{3}8,3 $$
Решение Вынеся общий множитель, получим:
$$\frac{1}{3}5,8+\frac{1}{3}8,3=\frac{1}{3}\left(5,8+ 8,3\right) =\frac{14,1}{3}=4,7$$
Ответ: 4,7.
Задание 2. Степень с рациональным показателем.
$$Упростите выражение \sqrt[3]{\sqrt[4]{a^{6}}} $$
Решение. Представим корни как степени с дробным показателем и сократим дробь в показателе:
$$\sqrt[3]{\sqrt[4]{a^{6}}}=\left(\left(a^{6} \right) \frac{1}{4} \right)^\frac{1}{3}=a^{\frac{6}{12}}=a^{\frac{1}{2}}=\sqrt{a}$$
$$Ответ: \sqrt{a}.$$
Задание 3. Степень с рациональным показателем.
$$ Вычислите 27^{\frac{2}{3}}-16^{\frac{1}{4}} $$
Решение. Представим дробные показатель как корни соответствующих степеней:
$$27^{\frac{2}{3}}-16^{\frac{1}{4}}=\sqrt[3]{27^{2}}-\sqrt[4]{16}=3^{2}-2=9-2=7 $$
Ответ: 7
Задание 4. Рациональные неравенства.
$$Решите неравенство \frac{x^{2}+11x+30}{x^{2}+3x-10}<0.$$ В ответ запишите наименьшее целое число, удовлетворяющее этому неравенству. Если такого числа нет, то в ответ запишите число 100.
Решение. Разложим числитель и знаменатель на множители, воспользовавшись теоремой Виета. $$\frac{\left(x+5 \right)\left(x+6 \right)}{\left(x+5 \right)\left(x-2 \right)}<0$$$$Отсюда ОДЗ: x\neq -5, x\neq 2. Теперь можно сократить на x+5$$$$ \frac{x+6}{x-2}<0$$
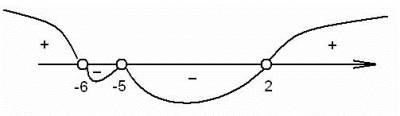
Чтобы сохранить знак, умножим на знаменатель в квадрате: (x+6)(x-2)<0.$$Воспользуемся методом интервалов Следовательно, x\epsilon \left(-6;-5 \right)\bigcup{}\left(-5;2 \right)$$
и наименьшим целым числом, удовлетворяющим неравенство, будет -4
Ответ: -4