Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида $$a_{11}x^2 + a_{22}y^2+2a_{12}xy+2a_{13}x+2a_{23}y+a_{33}=0,$$ в котором по крайней мере один из коэффициентов \(a_{11},\:a_{12},\:a_{22}\) отличен от нуля.

---

Вид кривой	Уравнение кривой	Примечание
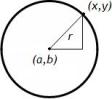
Окружность	$$(x-a)^2+(y-b)^2=r^2$$	Окружность - это множество точек плоскости, равноудаленных от данной точки (центра). \(r\) - радиус окружности, точка \(C(a,b)\) - ее центр.
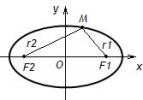
Эллипс	$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$	Эллипс - это множество точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная, причем эта постоянная больше расстояния между фокусами. \(a\) - большая, \(b\) - малая полуось эллипса, причем \(a,\;b\) и \(с\) (\(с\) - половина расстояния между фокусами) связаны соотношением \(a^2=b^2+c^2\).
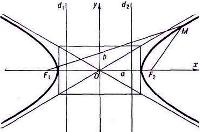
Гипербола	$$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$$	Гипербола - это множество точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная, причем эта постоянная меньше расстояния между фокусами. Причем \(b^2=c^2-a^2\).
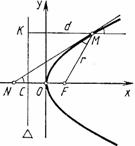
Парабола	$$y^2=2px$$	Парабола - это множество точек плоскости, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой. \(x=-p/2\) - директриса параболы, точка \(F(p/2;0)\) - фокус.

---