Вид поверхностиУравнение поверхности
Сфера $$(x-a)^2+(y-b)^2+(z-c)^2=R^2$$
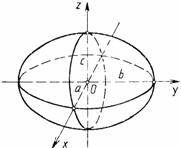
Эллипсоид $$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1 \;\; (a>0,\,b>0,\,c>0)$$
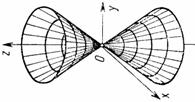
Конус второй степени $$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=0 \;\; (a>0,\,b>0,\,c>0)$$
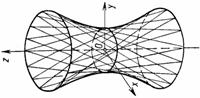
Однополостный гиперболоид $$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1 \;\; (a>0,\,b>0,\,c>0)$$
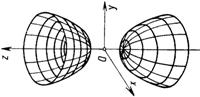
Двуполостный гиперболоид $$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=-1 \;\; (a>0,\,b>0,\,c>0)$$
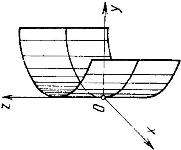
Эллиптический параболоид $$\frac{x^2}{p}+\frac{y^2}{q}=2z \;\; (p>0,\,q>0)$$
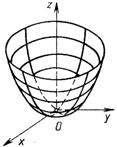Гиперболический параболоид $$\frac{x^2}{p}-\frac{y^2}{q}=2z \;\; (p>0,\,q>0)$$
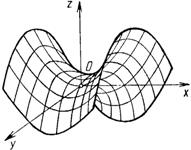Эллиптический цилиндр $$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \;\; (a>0,\,b>0)$$
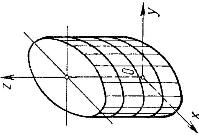Гиперболический цилиндр $$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \;\; (a>0,\,b>0)$$
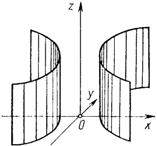Параболический цилиндр $$x^2=2py \;\; (p>0)$$

Оценка - 1.2 (46)
2010-12-21 • Просмотров [ 6635 ]