Интегралы от разрывных функций.
Если в интервале \([a, b]\) функция \(f(x)\) имеет некоторое число точек разрыва первого рода, то дать определение интеграла для такой функции не представляет никаких затруднений. В самом деле, при этом естественно считать, что интеграл есть просто сумма обыкновенных интегралов, взятых по частичным интервалам, на которые разбивается интервал \([a, b]\) всеми точками разрыва функции. Обозначив их через \(c_{1}, c_{2}, ...,c_{k}\), где \(b>c_{k}>...>c_{2}>c_{1}>a\), будем иметь $$\int_{a}^{b}{f(x)dx}=\int_{a}^{c_{1}}{f(x)dx}+\int_{c_{1}}^{c_{2}}{f(x)dx}+...+\int_{c_{k}}^{b}{f(x)dx}.$$
Этим самым дается и определение площади криволинейной трапеции, соответствующей функции \(y=f(x)\) с конечным числом точек разрыва первого рода в интервале \([a, b]\) (рис.1): площадь такой трапеции есть сумма площадей трапеции, опирающихся на частичные интервалы \([a, c_{1}], [c_{1}, c_{2}], ..., [c_{k}, b]\), заключенные между последовательными точками разрыва.
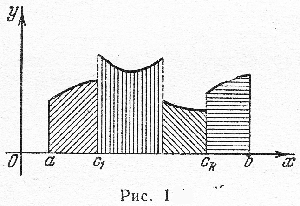
Перейдем к распространению определения интеграла для функций с бесконечными разрывами.
Пусть функция \(y=f(x)\) непрерывна для всех значений \(x\), \(b>x\geq a\), а в правом конце \(x=b\) интервала претерпевает бесконечный разрыв. Ясно, что обычное определение интеграла здесь теряет свой смысл. Но если взять обыкновенный интеграл
|
$$I(\varepsilon )=\int_{a}^{b-\varepsilon }{f(x)dx},$$
|
$$\varepsilon>0,$$
|
то мы можем считать, что \(I(\varepsilon )\) с уменьшением \(\varepsilon\) все лучше выражает ту величину, которую следует принять в качестве интеграла от функции \(f(x)\) в интервале \([a, b]\). Заставим \(\varepsilon\) стремиться к нулю. Тогда \(I(\varepsilon )\) либо имеет предел, либо не имеет (стремясь к бесконечности или вовсе не стремясь ни к какому пределу, т.е. колеблясь).
Определение. Несобственным интегралом от функции \(f(x)\), непрерывной при \(b>x\geq a\) и неограниченной при \(x\rightarrow b\), называется предел интеграла \(\int_{a}^{b-\varepsilon }{f(x)dx}\) при \(\varepsilon \rightarrow 0\).
Записывают это так:
|
$$\int_{a}^{b}{f(x)dx}=\lim_{\varepsilon \rightarrow 0}\int_{a}^{b-\varepsilon }{f(x)dx},$$
|
$$\varepsilon>0,$$
|
Если указанный предел существует, то несобственный интеграл называется сходящимся, а если не существует, то расходящимся.
Аналогично, если функция \(f(x)\) претерпевает бесконечный разрыв только в левом конце \(x=a\) интервала \([a, b]\), то
|
$$\int_{a}^{b}{f(x)dx}=\lim_{\delta \rightarrow 0}\int_{a+\delta }^{b}{f(x)dx},$$
|
$$\delta >0.$$
|
Если первообразная функция \(F(x)\) известна, то в обоих случаях можно записать, что $$\int_{a}^{b}{f(x)dx}=F(b)-F(a),$$
понимая под \(F(b)\) (или \(F(a)\)) предел, к которому стремится первообразная \(F(x)\) при \(x\rightarrow b\) (или при \(x\rightarrow a\)). Если этот предел не существует, то интеграл расходится.
Интегралы от разрывных функций. Примеры. Продолжение здесь