Интегралы от разрывных функций. Продолжение. Начало здесь

     Пример 1. $$\int_{0}^{a}{\frac{dx}{\sqrt{x}}}=2\sqrt{x}\mid _{0}^{a}=2\sqrt{a}.$$
     Пример 2. $$\int_{0}^{1}{\frac{dx}{1-x}}=-\ln (1-x)\mid _{0}^{1}$$
При \(x\rightarrow 1\) предел \(\ln (1-x)\) равен бесконечности; интеграл расходится.
     Вообще можно заметить, что интегралы

$$\int_{a}^{b}{\frac{dx}{(x-a)^{k}}}$$

и

$$\int_{a}^{b}{\frac{dx}{(b-x)^{k}}}$$

сходятся, если \(k<1\), и расходятся, если \(k\geq 1\).
     Пример 3. $$\int_{-1}^{1}{\frac{dx}{\sqrt{1-x^{2}}}}=arcsin x\mid _{-1}^{1}=\frac{\pi }{2}-(-\frac{\pi }{2})=$$
В этом примере подынтегральная функция имеет бесконечный разрыв на обоих концах интервала интегрирования.
     Если функция \(f(x)\) имеет бесконечный разрыв в какой-нибудь промежуточной точке \(x=c\) интервала \([a, b]\), \(b>c>a\), то по определению $$\int_{a}^{b}{f(x)dx}=\int_{a}^{c}{f(x)dx}+\int_{c}^{b}{f(x)dx}.$$
Если оба интеграла в правой части равенства сходятся, то сходится и интеграл \(\int_{a}^{b}{f(x)dx}\); этот интеграл расходится, если расходится хотя бы один из интегралов справа.
     Пример 4. $$\int_{-1}^{2}{\frac{dx}{\sqrt[3]{x^{2}}}}=\int_{-1}^{0}{\frac{dx}{\sqrt[3]{x^{2}}}}+\int_{0}^{2}{\frac{dx}{\sqrt[3]{x^{2}}}}=3\sqrt[3]{x}\mid _{-1}^{0}+3\sqrt[3]{x}\mid _{0}^{2}=3+3\sqrt[3]{2}.$$
     Пример 5. $$\int_{-1}^{1}{\frac{dx}{x^{2}}}=\int_{-1}^{0}{\frac{dx}{x^{2}}}+\int_{0}^{1}{\frac{dx}{x^{2}}}.$$
Оба интеграла справа расходятся, а значит, расходится и данный интеграл.
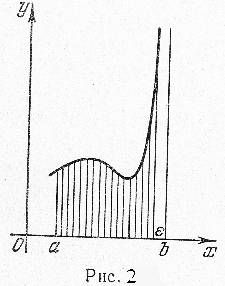
     Предположим, что функция \(y=f(x)\) имеет в точке \(x=b\) асимптоту, перпендикулярную к оси \(Ox\); тогда ограниченная ею трапеция будет бесконечной (с бесконечными высотами) (рис.2). Если существует несобственный интеграл от функции \(f(x)\), то считают, что он измеряет площадь этой бесконечной трапеции; в противном случае трапеция площади не имеет.

     Например, бесконечной трапеции,ограниченной линией \(y=\frac{1}{\sqrt{x}}\) и прямыми \(x=0\), \(x=a\), \(y=0\), можно приписать площадь, равную \(2\sqrt{a}\), ибо \(\int_{0}^{a}{\frac{dx}{\sqrt{x}}}=2\sqrt{a}\) (см. пример 1).
     Бесконечной же трапеции, ограниченной гиперболой \(y=\frac{1}{x}\) и теми же прямыми \(x=0\), \(x=a\), \(y=0\), нельзя приписать площади, ибо \(\int_{0}^{a}{\frac{dx}{x}}=\ln x\mid _{0}^{a}\) расходится.

---