Интегралы с бесконечными пределами. Продолжение. Начало здесь

Сходящимся несобственным интегралам можно придать определенный геометрический смысл. Пусть, например, график функции $y=f(x)$ ограничивает трапецию с бесконечным основанием (рис.1). Если несобственный интеграл $\int_{a}^{\propto }{f(x)dx}$ сходится, то будем говорить, что заштрихованная фигура имеет площадь, равную этому интегралу. Если интеграл расходится, то говорить о площади фигуры нельзя.

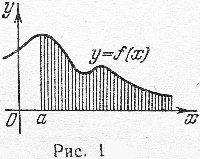
     Например, бесконечной трапеции, ограниченной положительной полуосью $Ox$, прямой $x=a$ ($a>0$) и линией $y=\frac{1}{x^{3}}$, можно приписать площадь, равную $\frac{1}{2a^{2}}$, ибо $$\int_{a}^{\propto }{\frac{1}{x^{3}}dx}=-\frac{1}{2}\frac{1}{x^{2}}\mid _{a}^{\propto }=\frac{1}{2a^{2}}.$$
     Бесконечной трапеции, ограниченной гиперболой $y=\frac{1}{x}$, положительной полуосью $Ox$ и прямой $x=a$ ($a>0$), нельзя приписать площадь, так как $$\int_{a}^{\propto }{\frac{1}{x}dx}=\ln x\mid _{a}^{\propto }=\propto.$$
     Несобственные интегралы рассмотренного типа часто встречаются в задачах механики и электростатики в связи с определением потенциала.
     Пусть точка $M$ массы $m$, находящаяся в начале координат, притягивает свободную точку $M_{1}$ массы $1$, лежащую на расстоянии $x$ от $M$ на оси $Ox$. Величина $P$ силы притяжения, как известно, определяется по зкону Ньютона

$$P=k\frac{m}{x^{2}},$$

где $k$ - константа,

а работа, произведенная при перемещении $M_{1}$ из точки $x=r$ в точку $x=b$ ($b>r>0$), - из формулы $$A=-\int_{r}^{b}{k\frac{m}{x^{2}}dx}=km(\frac{1}{b}-\frac{1}{r}).$$
Знак минус перед интегралом взят потому, что направление силы противоположно направлению движения точки $M$ (по той же причине работа оказалась отрицательной).
     Если точка удаляется в бесконечность ($b=\propto$), то $$A=-\int_{r}^{\propto }{k\frac{m}{x^{2}}dx}=-k\frac{m}{r}.$$
     Если точка $M_{1}$ будет перемещаться из бесконечности в точку $x=r$, то сила притяжения произведет уже положительную работу: $$A=k\frac{m}{r}.$$
     Эта работа называется потенциалом силы притяжения материальной точки $M$ при $x=r$ (или в точке $x=r$).

Оценка - 1.0 (13)

2012-11-09 • Просмотров [ 2059 ]

Интегралы с бесконечными пределами (продолжение)