Как и ранее, будем называть алфавитом \(A\) всякое непустое конечное множество символов, а сами символы алфавита будем называть буквами.
    Словом в алфавите \(A\) называется всякая конечная последовательность букв алфавита \(A\). Пустая последовательность букв называется пустым словом и обозначается через:

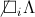
    Если \(P\) обозначает слово \(S_{j_{1}}S_{j_{2}}...S_{j_{k}}\) и \(Q\) обозначает слово \(S_{r_{1}}S_{r_{2}}...S_{r_{m}}\), то \(PQ\) обозначает объединение \(S_{j_{1}}...S_{j_{k}}S_{r_{1}}...S_{r_{m}}\). В частности, \(P\wedge =\wedge P=P\). Кроме тогo, \((P_{1}P_{2})P_{3}=P_{1}(P_{2}P_{3})\).
    Алфавит \(A\) называется расширением алфавита \(B\), если \(B\subset A\). Очевидно, что в этом случае всякое слово в алфавите является словом в алфавите \(A\).
    Алгоритмом в алфавите \(A\) называется эффективно вычислимая функция, областью определения которой служит какое-нибудь подмножество множества всех слов в алфавите \(A\) и значениями которой являются также слова в алфавите \(A\). Пусть \(P\) есть слово в алфавите \(A\); говорят, что алгоритм \(U\) применим к слову \(P\), если \(P\) содержится в области определения \(U\). Если алфавит \(B\) является расширением алфавита \(A\), то всякий алгоритм в алфавите \(B\) называется алгоритмом над алфавитом \(A\).
    Большинство известных алгоритмов можно разбить на некоторые простейшие шаrи. Следуя А. А. Маркову, в качестве элементарной операции, на базе которой строятся алгоритмы, выделим подстановку одного слова вместо другого. Если \(P\) и \(Q\) - слова в алфавите \(A\), то выражения \(P\rightarrow Q\) и \(P\rightarrow \cdot Q\) будем называть формулами подстановки в алфавите \(A\). При этом предполагается, что символы стрелка \(\rightarrow\) и точка \(\cdot\) не являются буквами алфавита \(A\), а каждое слово \(P\) и \(Q\) может быть и пустым словом. Формула подстановки \(P\rightarrow Q\) называется простой, а формула подстановки \(P\rightarrow \cdot Q\) называется заключительной.
    Пусть \(P \rightarrow (\cdot)Q\) обозначает одну из формул подстановки \(P\rightarrow Q\) или \(P\rightarrow \cdot Q\). Конечный список формул подстановки в алфавите $$\begin{cases} P_{1} \rightarrow (\cdot)Q _{1} \\ P _{2}\rightarrow (\cdot)Q _{2} \\ ................. \\ P_{r} \rightarrow (\cdot)Q_{r} \end{cases}$$
называется схемой алгоритма и порождает следующий алгоритм в алфавите \(A\).
    Принято говорить, что слово \(T\) входит в слово \(Q\), если существуют такие (возможно пустые) слова \(W\), \(V\), что \(Q=WTV\).
    Пусть \(P\) - слово в алфавите \(A\). Здесь может быть одно из двух:
    1. Ни одно из слов \(P_{1},P_{2},...,P_{r}\) не входит в слово \(P\) (обозначается: \(U : P \supset\)).
    2. Среди слов \(P_{1},P_{2},...,P_{r}\) существуют такие, которые входят в \(P\). Пусть \(m\) - наименьшее целое число такое, что \(1\leq m \leq r\), и \(P_{m}\) входит в \(P\), и \(R\) - слово, которое получается, если самое левое вхождение слова \(P_{m}\) в слово \(P\) заменить словом \(Q_{m}\). Тот факт, что \(P\) и \(Q\) находятся в описанном отношении, коротко запишем в виде

$$U : P \vdash R,$$

(a)

если формула подстановки \(P_{m}\rightarrow (\cdot ) Q_{m}\) - простая, или в виде

$$U : P \vdash \cdot R,$$

(b)

если формула \(P_{m}\rightarrow (\cdot ) Q_{m}\) - заключительная.
    В случае (а) говорят, что алгоритм \(U\) просто переводит слово \(P\) в слово \(R\); в случае (b) говорят, что алгоритм \(U\) заключительно переводит слово \(P\) в слово \(R\).
    Пусть далее, \(U :P \mid =R\) означает, что существует такая последовательность \(R_{0},R_{1},...,R_{k}\) слов в алфавите \(A\), что \(P=R_{0},R=R_{k}, U:R_{j}\vdash R_{j+1}\) для \(j=0,1,...,k-2\) и либо \(U:R_{k-1}\vdash R_{k}\), либо \(U:R_{k-1}\vdash \cdot R_{k}\) (в этом последнем случае вместо \(U:P\mid = R\) пишут \(U:P\mid = \cdot R\)).
    Положим теперь \(U(P)=R\) тогда и только тогда, когда либо \(U:P\mid = \cdot R\), либо \(U:P\mid = R\) и \(U:R\supset\).
    Алгоритм, определенный таким образом, называется нормальным алгоритмом или алгоритмом Маркова.
    Работа алгоритма \(U\) может быть описана следующим образом. Пусть дано слово \(P\) в алфавите \(A\). Находим первую в схеме алгоритма \(U\) формулу подстановки \(P_{m} \rightarrow (\cdot ) Q_{m}\), такую, что \(P_{m}\) входит в \(P\). Совершаем подстановку слова \(Q_{m}\) вместо самого левого вхождения слова \(P_{m}\) в слово \(P\). Пусть \(R_{1}\) - результат такой подстановки. Если \(P_{m} \rightarrow (\cdot ) Q_{m}\) - заключительная формула подстановки, то работа алгоритма заканчивается, и его значением является \(R_{1}\). Если формула подстановки \(P_{m} \rightarrow (\cdot ) Q_{m}\) - простая, то применим к \(R_{1}\) тот же поиск, который был только что применен к \(P\) и так далее. Если на конечном этапе будет получено такое слово \(R_{i}\), что \(U : R_{i} \supset\), то есть ни одно из слов \(P_{1},...,P_{r}\) не входит в \(R_{i}\), то работа алгоритма заканчивается, и \(R_{i}\) будет ero значением.
    Если описанный процесс на конечном этапе не заканчивается, то говорят, что алгоритм \(U\) не применим к слову \(P\).
    Пример 1. Пусть \(A\) есть алфавит \(\begin{Bmatrix} b,c \end{Bmatrix}\). Рассмотрим схему: $$\begin{cases} b\rightarrow \cdot \wedge \\ c \rightarrow c \end{cases}$$
    Определяемый этой схемой нормальный алгоритм \(U\) перерабатывает всякое слово \(P\) в алфавите \(A\), содержащее хотя бы одно вхождение буквы \(b\), в слово, которое получается вычеркиванием в \(P\) самого левого вхождения буквы \(b\).
    Действительно, всякая буква \(c\), находящаяся в слове левее самой левой буквы \(b\), простой подстановкой \(c\rightarrow c\) переводится в букву \(c\), а самая левая буква \(b\) заключительной подстановкой переводится в пустое слово.
    Например, если \(P=ccbbc\), то \(P\rightarrow \cdot Q\), где \(Q=ccbc\).
    Пустое слово \(U\) перерабатывает в само себя.
    \(U\) не применим к непустым словам, не содержащим вхождения буквы \(b\) . Действительно, если слово \(P\) содержит только буквы \(c\), то простой подстановкой \(c\rightarrow c\) оно будет перерабатываться в себя, но тогда всегда \(P \rightarrow P\), и мы не приходим к заключительной подстановке, то есть процесс будет продолжаться бесконечно.
    Пример 2. Пусть \(A\) есть алфавит \(\begin{Bmatrix} a_{0}, a_{1},...,a_{n} \end{Bmatrix}\). Рассмотрим схему: $$\forall i ( a_{i} \rightarrow \wedge ) (a_{i} \epsilon A).$$
    Эта схема определяет нормальный алгоритм \(U\), перерабатывающий всякое слово в алфавите \(A\) в пустое слово. Например, $$U:a_{1}a_{2}a_{1}a_{3}a_{0}\vdash a_{1}a_{2}a_{1}a_{3} \vdash a_{2}a_{1}a_{3}\vdash a_{2}a_{3}\vdash a_{3} \wedge ,$$
и, наконец, \(U: \wedge \supset\). Следовательно, \(U(a_{1}a_{2}a_{1}a_{3}a_{0}) = \wedge\).

---