Дисперсия, среднее квадратическое отклонение

    Из всех моментов в качестве характеристик случайной величины чаще всего применяются первый начальный момент (математическое ожидание) \(m_{x}=a_{1}\)и второй центральный момент \(\mu _{2}\).
    Второй центральный момент называется дисперсией случайной величины. Ввиду крайней важности этой характеристики среди других моментов введем для нее специальное обозначение \(D[X]\):

$$\mu _{2}=D[X]$$ Согласно определению центрального момента $$D[X]=M[X^{2}]$$ т. е. дисперсией случайной величины \(X\) называется математическое ожидание квадрата соответствующей центрированной величины.
    Для непосредственного вычисления дисперсии служат формулы: $$D[X]=\sum_{i=1}^{n}{(x_{i}-m_{x})^{2}p_{i}}$$ $$D[X]=\int_ {-\infty}^{\infty}{(x-m_{x})^{2}f(x)dx}$$ — соответственно для прерывных и непрерывных величин.
    Дисперсия случайной величины есть характеристика рассеивания, разбросанности значений случайной величины около ее математического ожидания. Само слово «дисперсия» означает «рассеивание».
    Если обратиться к механической интерпретации распределения, то дисперсия представляет собой не что иное, как момент инерции заданного распределения масс относительно центра тяжести (математического ожидания).
    Дисперсия случайной величины имеет размерность квадрата случайной величины; для наглядной характеристики рассеивания удобнее пользоваться величиной, размерность которой совпадает с размерностью случайной величины. Для этого из дисперсии извлекают квадратный корень. Полученная величина называется средним квадратическим отклонением (иначе—«стандартом») случайной величины \(X\). Среднее квадратическое отклонение будем обозначать \(\sigma[X]\): $$\sigma[X]=\sqrt {D[X]}$$     Математическое ожидание \(m_{x}\) и дисперсия \(D_{x}\) (или среднее квадратическое отклонение \(\sigma_{x}\)) — наиболее часто применяемые характеристики случайной величины. Они характеризуют наиболее важные черты распределения: его положение и степень разбросанности. Для более подробного описания распределения применяются моменты высших порядков.
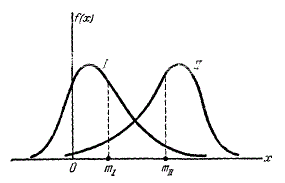
    Третий центральный момент служит для характеристики асимметрии (или «скошенности») распределения. Если распределение симметрично относительно математического ожидания (или, в механической интерпретации, масса распределена симметрично относительно центра тяжести), то все моменты нечетного порядка (если они существуют) равны нулю. Действительно, в сумме $$\mu _{s}=\sum_{i=1}^{n}{(x_{i}-m_{x})}^{S}p_{i}$$ при симметричном относительно \(m_{x}\) законе распределения и нечетном \(S\) каждому положительному слагаемому соответствует равное ему по абсолютной величине отрицательное слагаемое, так что вся сумма равна нулю. То же, очевидно, справедливо и для интеграла $$\mu _{s}=\int_ {-\infty}^{\infty}{(x-m_{x})^{S}f(x)dx}$$ который равен нулю, как интеграл в симметричных пределах от нечетной функции.
    Естественно поэтому в качестве характеристики асимметрии распределения выбрать какой-либо из нечетных моментов. Простейший из них есть третий центральный момент. Он имеет размерность куба случайной величины; чтобы получить безразмерную характеристику, третий момент \(\mu _{3}\) делят на куб среднего квадратического отклонения.
    Полученная величина носит название «коэффициента асимметрии» или просто «асимметрии»; мы обозначим ее \(Sk\): $$Sk=\frac{\mu_{3}}{\sigma _{3}}$$ Ha рис.1 показано два асимметричных распределения; одно из них (кривая 1) имеет положительную асимметрию (\(Sk > 0\)); другая (кривая 2) - отрицательную (\(Sk < 0\)).
    Четвертый центральный момент служит для характеристики так называемой «крутости», т. е. oстровершинности или плосковершинности распределения. Эти свойства распределения описываются с помощью так называемого эксцесса. Эксцессом случайной величины \(X\) называется величина $$Ex=\frac{\mu_{4}}{\sigma _{4}}-3.$$
    Число \(3\) вычитается из отношения \(\frac{\mu_{4}}{\sigma _{4}}\), потому что для весьма важного и широко распространенного в природе нормального закона распределения (с которым мы подробно познакомимся в дальнейшем) \(\frac{\mu_{4}}{\sigma _{4}}=3\).
    Таким образом для нормального распределения эксцесс равен нулю; кривые, более островершинные по сравнению с нормальной, обладают положительным эксцессом; кривые более плосковершинные — отрицательным эксцессом.
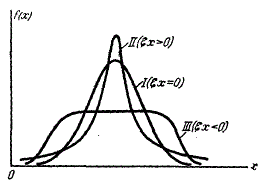
    На рис. 2 представлены: нормальное распределение (кривая 1), распределение с положительным эксцессом (кривая 2) и распределение с отрицательным эксцессом (кривая 3).

---