Функция распределения системы двух случайных величин

    Функцией распределения системы двух случайных величин \((X, Y)\) называется вероятность совместного выполнения двух неравенств \(Х<х\) и \(У<у\):

$$F(x,y)=P((X < x)(Y< y))$$     Если пользоваться для геометрической интерпретации системы образом случайной точки, то функция распределения \(F(x, у)\) есть не что иное, как вероятность попадании случайной точки \((X, Y)\) в бесконечный квадрант с вершиной в точке \((х, у)\), лежащий левее и ниже ее (рис.1).     В аналогичной интерпретации функция распределения одной случайной величины \(X\) — обозначим ее \(F_{1}(x)\) — представляет собой вероятность попадания случайной точки в полуплоскость, ограниченную справа абсциссой \(х\); функция распределения одной величины \(Y\) — \(F_{2}(y)\) — вероятность попадания в полуплоскость, ограниченную сверху ординатой у (рис. 2).
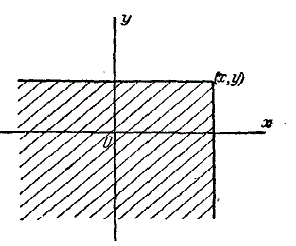
    Сформулируем аналогичные свойства для функции распределения системы случайных величин и снова воспользуемся геометрической интерпретацией для наглядной иллюстрации этих свойств.
    1. Функция распределения \(F(x, у)\) есть неубывающая функция обоих своих аргументов, т. е.
при \(x_{2} > x_{1}\)  \(F(x_{2},y) \geq F(x_{1},y)\)
при \(y_{2} > y_{1}\)  \(F(x,y_{2}) \geq F(x,y_{1})\)
    В этом свойстве функции \(F (х)\) можно наглядно убедиться, пользуясь геометрической интерпретацией функции распределения как вероятности попадания в квадрант с вершиной \((х, у)\) (рис.1).
    2. Повсюду на \(- \infty\) функция распределения равна нулю: $$F(x, -\infty)=F(-\infty, y)=F(- \infty, -\infty)=0$$     В этом свойстве мы наглядно убеждаемся, неограниченно отодвигая влево правую границу квадранта \((x\rightarrow -\infty)\) или вниз его верхнюю границу \((y\rightarrow -\infty)\) или делая это одновременно с обеими границами; при этом вероятность попадания в квадрант стремится к нулю.
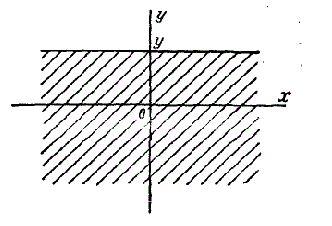
    3. При одном из аргументов, равном \(+\infty)\), функция распределения системы превращается в функцию распределения случайной величины, соответствующей другому аргументу:
\(F(x, +\infty)=F_{1}(x)\),  \(F(y, +\infty)=F_{2}(y)\)
где \(F_{1}(x), F_{2}(y)\) — соответственно функции распределения случайных величин \(X\) и \(Y\).
    В этом свойстве функции распределения можно наглядно убедиться, смещая ту или иную из границ квадранта на \(+\infty\); при этом в пределе квадрант превращается в полуплоскость, вероятность попадания в которую есть функция распределения одной из величин, входящих в систему.
    4. Если оба аргумента равны \(+\infty\), функция распределения системы равна единице: $$F(+\infty, +\infty)=1$$     Действительно, при \((x\rightarrow +\infty)\),\((y\rightarrow +\infty)\) квадрант с вершиной \((х, у)\) в пределе обращается во всю плоскость \(xOy\), попадание в которую есть достоверное событие.     

---