Плотность распределения системы двух случайных величин

    Введенная в предыдущем характеристика системы — функция распределения — существует для систем любых случайных величин, как преривиых, так я непрерывных. Основное практическое значение имеют системы непрерывных случайных величин. Распределение системы непрерывных величин обычно характеризуют не функцией распределения, а плотностью распределения.
    Вводя в рассмотрение плотность распределения для одной случайной величины, мы определяли ее как предел отношения вероятности попадания на малый участок к длине этого участка при ее неограниченном уменьшении. Аналогично определим плотность распределения системы двух величин.
    Пусть имеется система двух непрерывных случайных величин \((X, Y)\), которая интерпретируется случайной точкой на плоскости \(хОу\). Рассмотрим на этой плоскости малый прямоугольник \(R \Delta\) со сторонами \(\Delta x\) и \(\Delta y\), примыкающий к точке с координатами \((х, у)\) (рис. 1).

Вероятность попадания в этот прямоугольник по формуле равна $$P((X, Y)\subset R \Delta )= F(x+ \Delta x, y+ \Delta y)- F(x+ \Delta x, y)-F(x, y+ \Delta y)+F(x, y)$$     Разделим вероятность попадания в прямоугольник \(R \Delta\) на площадь этого прямоугольника и перейдем к пределу при \(\Delta x\rightarrow 0\) и \(\Delta y\rightarrow 0\): $$\lim_{\Delta x\rightarrow 0 \Delta y\rightarrow 0}\frac{P((X, Y)\subset R \Delta )}{\Delta x \Delta y}= \frac{F(x+ \Delta x, y+ \Delta y)- F(x+ \Delta x, y)-F(x, y+ \Delta y)+F(x, y)}{\Delta x \Delta y}$$     Предположим, что функция \(F(x, у)\) не только непрерывна, но и дифференцируема; тогда правая часть формулы представляет собой вторую смешанную частную производную функции \(F (х, у)\) по \(х\) и \(у\). Обозначим эту производную \(f(x, y)\): $$f(x,y)=\frac{\partial^{2}F(x,y) }{\partial x \partial y}=F''_{xy}(x, y)$$     Функция \(f (х, у)\) называется плотностью распределения системы.
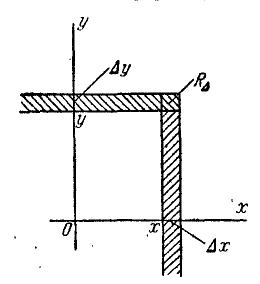
    Таким образом, плотность распределения системы представляет собой предел отношения вероятности попадания в малый прямоугольник к площади этого прямоугольника, когда оба его размера стремятся к нулю; она может быть выражена как вторая смешанная частная производная функции распределения системы по обоим аргументам.
    Если воспользоваться «механической» интерпретацией распределения системы как распределения единичной массы по плоскости \(хОу\), функция \(f(x, у)\) представляет собой плотность распределения массы в точке \((х, у)\).
    Геометрически функцию \(f(x, у)\) можно изобразить некоторой поверхностью (рис.2). Эта поверхность аналогична кривой распределения для одной случайной величины и называется поверхностью распределения.
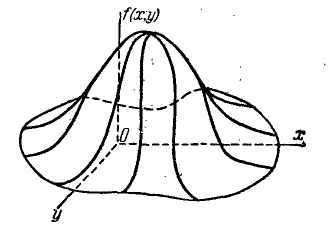
    Если пересечь поверхность распределения \(f(x, у)\) плоскостью, параллельной плоскости \(хОу\), и спроектировать полученное сечение на плоскость \(хОу\), получится кривая, в каждой точке которой плотность распределения постоянна. Такие кривые называются кривыми равной плотности. Кривые равной плотности, очевидно, представляют собой горизонтали поверхности распределения задавать распределение семейством кривых. Часто бывает удобно задавать распределение семейством кривых равной плотности.
    Рассматривая плотность распределения \(f(x)\) для одной случайной величины, мы ввели понятие «элемента вероятности» \(f(x)dx\). Это есть вероятность попадания случайной величины \(X\) на элементарный участок \(dx\), прилежащий к точке \(х\). Аналогичное понятие «элемента вероятности» вводится и для системы двух случайных величин. Элементом вероятности в данном случае называется выражение $$f(x,y)dx dy$$
    Очевидно, элемент вероятности есть не что иное, как вероятность попадания в элементарный прямоугольник со сторонами \(dx, dy\) примикающий к точке \((х, у)\) (рис. 3). Эта вероятность равна объему элементарного параллелепипеда, ограниченного сверху поверхностью \(f(x, у)\) и опирающегося на элементарный прямоугольник \(dx dy\) (рис. 4).
    Пользуясь понятием элемента вероятности, выведем выражение для вероятности попадания случайной точки в произвольную область \(D\). Эта вероятность, очевидно, может быть получена суммированием (интегрированием) элементов вероятности по всей области \(D\).
    Геометрически вероятность попадания в область \(D\) изображается объемом цилиндрического тела \(С\), ограниченного сверху поверхностью распределения и опирающегося на область \(D\).
    Легко убедиться в следующих свойствах плотности распределения системы:
    1. Плотность распределения системы есть функция неотрицательная: $$f(x,y) \geq 0$$      Это ясно из того, что плотность распределения есть предел отношения двух неотрицательных величин: вероятности попадания в прямоугольник и площади прямоугольника — и, следовательно, отрицательной быть не может.
    2. Двойной интеграл в бесконечных пределах от плотности распределения системы равен единице: $${\int\int}_{-\infty}^{+\infty}f(x,y) dxdy=1$$     Это видно из того, что интеграл есть не что иное, как вероятность попадания во всю плоскость \(хОу\), т. е. вероятность достоверного события.
    Геометрически это свойство означает, что полный объем тела, ограниченного поверхностью распределения и плоскостью \(хОу\), равен единице.

---