Примеры на построение функции распределения

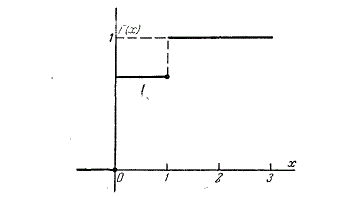
    Пример 1. Производится один опыт, в котором может появиться или не появиться событие \(A\). Вероятность события \(A\) равна \(0,3\). Случайная величина \(X\) — число появлений события \(A\) в опыте (характеристическая случайная величина события \(A\)). Построить ее функцию распределения.
    Решение. Ряд распределения величины \(X\) имеет вид:

\(x_{i}\)	\(0\)	\(1\)
\(p_{i}\)	\(0,7\)	\(0,3\)

    Построим функцию распределения величины \(X\):
1) при \(x\leq 0\) $$F(x)=P(X< x)=0$$ 2) при \(0< x\leq 1\) $$F(x)=P(X< x)=P(X=0)=0,7$$ 3) при x >1 $$F(x)=P(X< x)=P(X=0)+P(X=1)=1.$$     График функции распределения представлен на рис.1. В точках разрыва функция \(F(x)\) принимает значения, отмеченные на чертеже точками (функция непрерывна слева). Рис.1.
    Пример 2. В условиях предыдущего примера производится независимых опыта. Построить функцию распределения числа появлений события \(A\).
    Решение. Обозначим \(X\) — число появлений события \(A\) в четырех опытах. Эта величина имеет ряд распределения:

\(x_{i}\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)
\(p_{i}\)	\(0,2401\)	\(0,4116\)	\(0,2646\)	\(0,0756\)	\(0,0081\)

    Построим функцию распределения случайной величины \(X\):
1) при \(x\leq 0\)   \(F(x)=0\);
2) при \(0< x\leq 1\)   \(F(x)=0,2401\);
3) при \(1< x\leq 2\)   \(F(x)=0,6517\);
4) при \(2< x\leq 3\)   \(F(x)=0,9163\);
5) при \(3< x\leq 4\)   \(F(x)=0,9919\);
6) при \(x >4\)   \(F(x)=1\).
    График функции распределения представлен на рис.2. Рис.2.
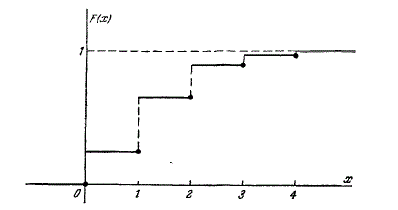
    Функция распределения любой прерывной случайной величины всегда есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины, и равны вероятностям этих значений. Сумма всех скачков функции \(F(x)\) равна единице.

---