Примеры прерывных случайных величин с их законами распределения

    Пример 1. Производится один опыт, в котором может появиться или не появиться событие \(A\). Вероятность событий \(A\) равна \(0,3\). Рассматривается случайная величина \(X\) - число появлений события \(A\) в данном опыте (т.е. характеристическая случайная величина события \(A\), принимающая значение \(1\), если оно появится, и \(0\), если не появится). Построить ряд распределения и многоугольник распределения величины \(X\).
    Решение. Величина \(X\) имеет всего два значения: \(0\) и \(1\). Ряд распределения величины \(X\) имеет вид:

\(x_{i}\)	\(0\)	\(1\)
\(p_{i}\)	\(0,7\)	\(0,3\)

    Многоугольник распределения изображен на рис.1. 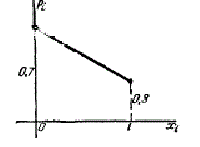Рис.1.

    Пример 2. Стрелок ведет стрельбу по мишени до первого попадания , имея боезапас \(4\) патрона. Вероятность попадания при каждом выстреле равна \(0,6\). Построить ряд распределения боезапаса, оставшегося неизрасходованным.
    Решение. Случайная величина \(X\) – число неизрасходованных патронов – имеет четыре возможных значения: \(0, 1, 2 и 3\). Вероятность этих значений равны соответственно:

$$p_{0}=0,4^3=0,064;$$ $$p_{1}=0,4^2\cdot 0,6=0,096;$$ $$p_{2}=0,4\cdot 0,6=0,24;$$ $$p_{3}=0,600.$$     Ряд распределения величины \(X\) имеет вид:

\(x_{i}\)	\(0\)	\(5\)	\(10\)	\(15\)
\(p_{i}\)	\(0,216\)	\(0,432\)	\(0,288\)	\(0,064\)

    Многоугольник распределения показан на рис.2. 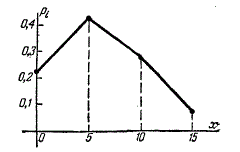Рис.2.

    Пример 3. Техническое устройство может применяться в различных условиях и в зависимости от этого время от времени требует регулировки. При однократном применении устройства оно может случайным образом попасть в благоприятный или неблагоприятный режим. В благоприятном режиме устройство выдерживает три применения без регулировки; перед четвертым его приходится регулировать. В неблагоприятном режиме устройство приходится регулировать после первого же применения. Вероятность того, что устройство попадет в благоприятный режим, - \(0,7\), что в неблагоприятный, - \(0,3\). Рассматривается случайная величина \(X\) - число применений устройства до регулировки. Построить ее ряд распределения.
    Решение. Случайная величина \(X\) имеет три возможных значения: \(1, 2, 3\). Вероятность того, что \(X=1\), равна вероятности того , что при первом же применении устройство попадет в неблагоприятный режим , т.е. \(p_{1}=0,3\). Для того чтобы величина \(X\) приняла значение \(2\) нужно, чтобы при первом применении устройство попало в благоприятный режим, а при втором - в неблагоприятный; вероятность этого \(p_{2}=0,7\cdot 0,3=0,21\). Чтобы величина \(X\) приняла значение \(3\), нужно, чтобы два первых раза устройство попало в благоприятный режим ( после третьего раза его все равно придется регулировать). Вероятность этого равна \(p_{3}=0,7^2=0,49\).
    Ряд распределения величины имеет вид:

\(x_{i}\)	\(1\)	\(2\)	\(3\)
\(p_{i}\)	\(0,3\)	\(0,21\)	\(0,49\)

    Многоугольник распределения показан на рис.3. 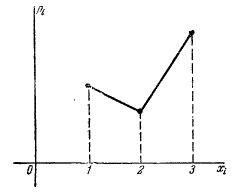Рис.3.

---