Исследование функции - типовая задача высшей математики. Требуется выполнить анализ её поведения (область определения, точки экстремума, пересечения с осями, выпуклость и асимптоты), а затем построить график. С помощью Wolfram Language используя ChatGPT мы можем эффективно проводить подобное исследование, автоматизируя расчёты и визуализацию. Покажем здесь на конкретном примере как это можно сделать.
Важно. И вот тут самое интересное - вы можете попросить ChatGPT и Wolfram написать все команды для исследования и тут же выполнять все эти команды. Вам не надо ни устанавливать WOLFRAM ли покупать платную версию, ни подключаться к облачной версии. ChatGPT спросит у вас разрешение подключиться к облаку и сделает все вычисления и построения сам. И построит график. Смотрите ниже как все это работает. Сразу приводим команду Wolfram Language и результат ее выполнения.
Пошаговый процесс исследования
1. Определение функции
Начнем с задания функции. Например:
$$ f(x) = x^3 - 6x^2 + 9x + 1 $$
f[x_] := x^3 - 6x^2 + 9x + 12. Область определения
Для проверки области определения функции используем:
domain = Reduce[f[x] ∈ Reals, x, Reals]Функция определена на всём множестве действительных чисел:
$$ \text{Domain: } (-\infty, +\infty) $$
3. Найдём пересечения с осями
Пересечения с осью \( x \) (нулевые точки):
xIntercepts = Solve[f[x] == 0, x]Пересечения с осью \(x\):
$$ x = 1 \text{ (кратность 2), } x = -1 $$
Пересечение с осью \( y \):
yIntercept = f[0]Пересечение с осью \(y\):
$$ f(0) = 1 $$
4. Исследование производных
Первая производная:
fPrime = f'[x]Найдем критические точки (где \( f'(x) = 0 \)):
criticalPoints = Solve[fPrime == 0, x]Первая производная:
$$ f'(x) = 3x^2 - 12x + 9 $$
Критические точки:
$$ x = 1 \text{ (минимум), } x = 3 \text{ (максимум)} $$
Исследуем вторую производную:
fDoublePrime = f''[x]Определим точки перегиба (где \( f''(x) = 0 \)):
inflectionPoints = Solve[fDoublePrime == 0, x]Вторая производная:
$$ f''(x) = 6x - 12 $$
Точки перегиба:
$$ x = 2 $$
5. Исследование асимптот
Для анализа горизонтальных, вертикальных и наклонных асимптот используем:
asymptotes = Limit[f[x], x -> Infinity]Асимптоты:
Горизонтальные и наклонные асимптоты отсутствуют.
При \( x \to \infty, f(x) \to \infty \).
6. Построение графика функции
Используем команду:
Plot[f[x], {x, -2, 6}, PlotRange -> All]График функции:
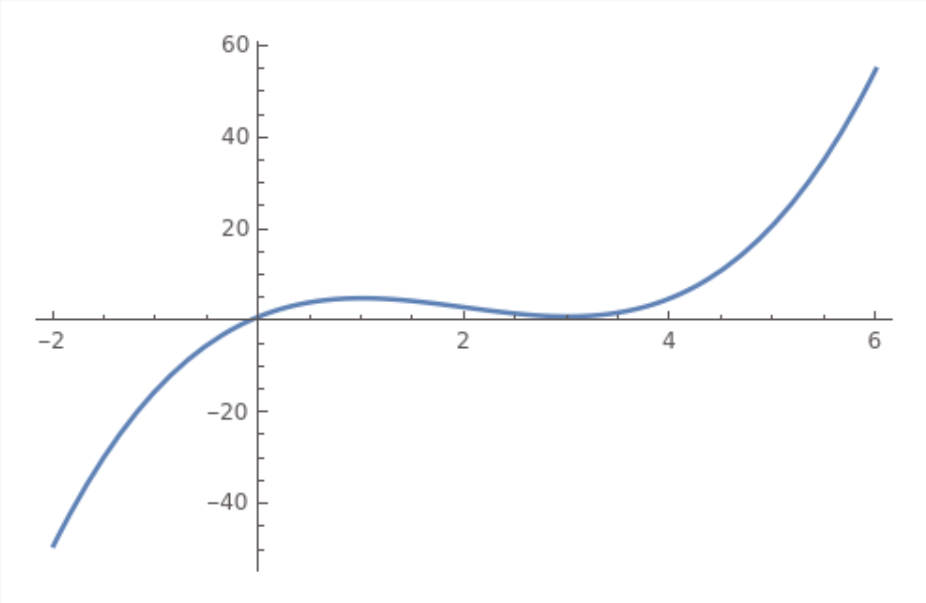
Пример команд полного исследования
Приведем здесь полный набор команд Wolfram Language для выполнения исследования и построения графика функции.
Проведём анализ функции \( f(x) = x^3 - 6x^2 + 9x + 1 \).
f[x_] := x^3 - 6x^2 + 9x + 1
domain = Reduce[f[x] ∈ Reals, x, Reals]
xIntercepts = Solve[f[x] == 0, x]
yIntercept = f[0]
fPrime = f'[x]
criticalPoints = Solve[fPrime == 0, x]
fDoublePrime = f''[x]
inflectionPoints = Solve[fDoublePrime == 0, x]
asymptotes = Limit[f[x], x -> Infinity]
Plot[f[x], {x, -2, 6}, PlotRange -> All]
Бонус. А для тех, кто дочитал сюда, приводим ссылку на чат ChatGPT с кодом этого исследования (у вас должен быть аккаунт).
Подведем итоги
Используя Wolfram Language, мы можем быстро анализировать функции, находить важные характеристики и строить их графики. Для этого достаточно следовать указанной последовательности шагов и применять соответствующие команды.
