Графічний ключ є популярним способом захисту доступу до смартфона чи окремих додатків. Він базується на 9 точках, розташованих у квадратній сітці 3×3, через які користувач проводить певне графічне зображення. Дослідження кількості можливих комбінацій графічних ключів базується на принципах комбінаторики та враховує кілька умов. У цій статті ми розглянемо, як підраховується кількість варіантів такого ключа.
Умови побудови графічного ключа
Основні правила створення графічного ключа:
- Ключ має складатися щонайменше з 4 точок.
- Кожна точка може бути використана лише один раз.
- Якщо між двома точками знаходиться інша точка, вона має бути пройдена першою.
Ці обмеження впливають на кількість можливих комбінацій ключа, оскільки деякі шляхи між точками стають недоступними.
Приклад створення графічного ключа
Розглянемо приклад графічного ключа, який включає п'ять точок. Зображення матриці з напрямками руху:
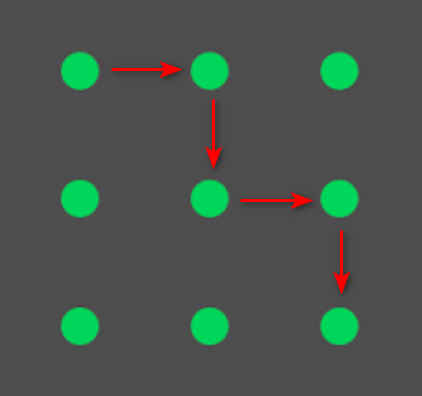
Пояснення руху:
- Початок ключа: верхній лівий кут (⦿).
- Рух: вправо до центральної точки у верхньому ряду, потім униз.
- Наступний рух: до правої точки третьої колонки.
- Фінальний рух: вниз у третій ряд.
Основи комбінаторики для підрахунку
Для аналізу використовуємо формули комбінаторики. Графічний ключ є упорядкованою послідовністю точок, тому кількість комбінацій залежить від кількості доступних точок та їх порядку в ключі.
Використовуємо формулу для кількості перестановок:
$$P(n, k) = \frac{n!}{(n-k)!},$$
де:
- \(n\) — загальна кількість точок (9),
- \(k\) — кількість точок у ключі.
Кількість ключів для різних довжин
Розраховуємо можливу кількість ключів для кожної допустимої довжини:
- Для 4 точок: \(P(9, 4) = \frac{9!}{(9-4)!} = \frac{9 \cdot 8 \cdot 7 \cdot 6}{1} = 3024\).
- Для 5 точок: \(P(9, 5) = \frac{9!}{(9-5)!} = 15120\).
- Для 6 точок: \(P(9, 6) = \frac{9!}{(9-6)!} = 60480\).
- Для 7 точок: \(P(9, 7) = \frac{9!}{(9-7)!} = 181440\).
- Для 8 точок: \(P(9, 8) = \frac{9!}{(9-8)!} = 362880\).
- Для 9 точок: \(P(9, 9) = 9! = 362880\).
Підсумуємо результати:
$$N = P(9, 4) + P(9, 5) + P(9, 6) + P(9, 7) + P(9, 8) + P(9, 9),$$
$$N = 3024 + 15120 + 60480 + 181440 + 362880 + 362880 = 985824.$$
Врахування додаткових обмежень
На практиці кількість можливих ключів менша через обмеження на прямі лінії через середні точки. Наприклад, якщо ви хочете провести лінію від верхньої лівої точки до верхньої правої, то середня точка має бути пройдена. Такі випадки враховуються спеціальними алгоритмами, які моделюють усі можливі шляхи. В інтернеті стверджується, що загальна кількість можливих ключів, які відповідають усім умовам, становить 389112. Але чи це так? Пишіть ваші варіанти в коментарі.
«Безпека — це не продукт, а процес.»
Натяк на майбутнє
Графічні ключі — це не лише про безпеку, а й про зручність. У майбутньому можливі зміни у дизайні таких систем захисту, наприклад, додавання кольорів або ускладнення правил. Це відкриває цікаві перспективи для дослідження.
Схожі публікації
