Математическое ожидание, мода, медиана (продолжение) Начало здесь

    Для непрерывной величины \(X\) математическое ожидание, естественно, выражается уже не суммой, а интегралом:

$$M[X]=\int_{-\infty}^{\infty}{xf(x)dx},$$ где \(f(x)\) - плотность распределения величины \(X\).
    В механической интерпретации математическое ожидание непрерывной случайной велчины сохраняет тот же смысл - абсцисс непрерывно, с плотностью \(f(x)\). Эта интерпретация часто позвояет найти математическое ожидание без вычисления интеграла.
    Выше мы ввели обозначение \(M[X]\) для математического ожидания величины \(X\). В ряде случаев, когда величина \(M[X]\) входит в формулы как определенное число, ее удобнее обозначить одной буквой. В этих случаях мы будем обозначать математическое ожидание величины \(X\) через \(m_{x}\): $$m_{x}=M[X]$$
    Обозначения \(m_{x}\) и \(M[X]\) для математического ожидания будут в дальнейшем применяться параллельно в зависимости от удобства той или иной записи формул.
    Следует заметить, что важнейшая характеристика положения - математическое ожидание - существует не для всех случайных величин. Можно составить примеры таких случайных величин, для которых математическое ожидание не существует, так как соответствующая сума или интеграл расходятся.
    Рассмотрим, например, прерывную случайную величину \(X\) с рядом распределения:

\(x_{i}\)	\(2\)	\(2^{2}\)	\(...\)	\(2_{i}\)
\(p_{i}\)	\(\frac{1}{2}\)	\(\frac{1}{2^{2}}\)	\(...\)	\(\frac{1}{2^{i}}\)

    Нетрудно убедиться в том, что, \(\sum_{i=1}^{n}{p_{i}}=1\), т. е. ряд распределения имеет смысл; однако сумма \(\sum_{i=1}^{\infty}{x_{i}p_{i}}\) в данном случае расходится и, следовательно, математического ожидания величины \(X\) не существует. Однако для практики такие случаи существенного интереса не представляют. Обычно случайные величины, с которыми мы имеем дело, имеют ограниченную область возможных значений и безусловно обладают математическим ожиданием.
    Если величина \(X\) принадлежит к величинам смешанного типа, то ее математическое ожидание выражается формулой вида: $$M[X]=\sum_{i}{x_{i}p_{i}}+\int x\acute{F}(x)dx$$ где сумма распространяется на нее точки \(x_{i}\), в которых функция распределения терпит разрыв, а интеграл — на все участки, на которых функция распределения непрерывна.
    Кроме важнейшей из характеристик положения — математического ожидания, — на практике иногда применяются и другие характеристики положения, в частности мода и медиана случайной величины.
    Модой случайной величины называется ее наиболее вероятное значение. Термин «наиболее вероятное значение», строго говоря, применим только к прерывным величинам; для непрерывной величины модой является то значение, в котором плотность вероятности максимальна. Условимся обозначать моду буквой \(\mathit{M}\). На рис. 1 и 2 показана мода соответственно для прерывной и непрерывной случайных величин. Рис.1 - для прерывной случайной величины Рис.2 - для непрерывной случайной величины
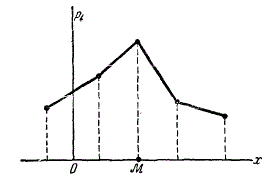
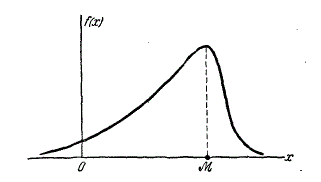
    Часто применяется еще одна характеристика положения — так называемая медиана случайной величины. Этой характеристикой пользуются обычно только для непрерывных случайных величин, хотя формально можно ее определить и для прерывной величины.
    Медианой случайной величины \(X\) называется такое ее значение \(\mathit{Me}\), для которого $$P(X< \mathit{Me})=P(X>\mathit{Me}),$$ Рис.3 - медиана случайной величины т. е. одинаково вероятно, окажется ли случайная величина меньше или больше \(\mathit{Me}\). Геометрическая медиана — это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам (рис. 3).
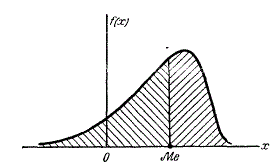
    В случае симметричного модального распределения медиана совпадает с математическим ожиданием и модой.

---