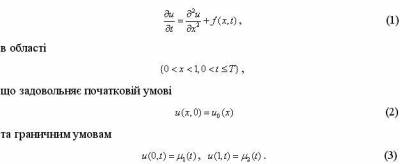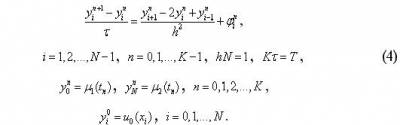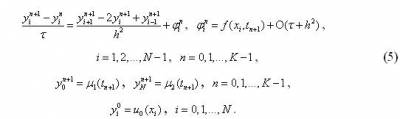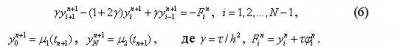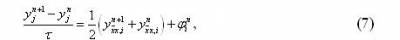Різницеві схеми для рівняння теплопровідності
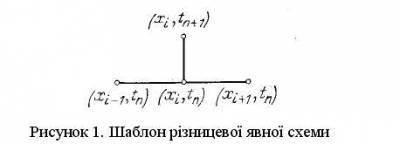
1. Розглянемо наступну першу крайову задачу для рівняння теплопровідності з постійними коефіцієнтами. Потрібно знайти розв’язок рівняння
Тут u0(x), μ1(t), μ2(t) − задані функції. Відомо, що при визначених припущеннях гладкості існує єдиний розв’язок задачі (1)-(3). Розв’язок задачі (1)-(3) задовольняє принципу максимуму і тим самим безперервно залежить від початкових та граничних даних.
2. Явна схема. Для побудови різницевої схеми потрібно перш за все ввести сітку в області зміни незалежних змінних та задати шаблон, тобто множину точок сітки, які приймають участь в апроксимації диференціального виразу. Для того щоб апроксимувати рівняння (1) в точці (xi, tn) введемо шаблон зображений на рисунку 1, який складається з чотирьох вузлів.
Під поняттям різницевої схеми розуміють сукупність різницевих рівнянь, що апрксимують основне диференціальне рівняння в усіх внутрішніх вузлах сітки та додаткові (початкові та граничні) умови − у граничних вузлах сітки. Різницеву схему за аналогією з диференціальною задачею будемо називати також різницевою задачею. Явна різницева схема для заданого рівняння теплопровідності матиме наступний вигляд
Це схема лінійних алгебраїчних рівнянь з числом рівнянь, що дорівнює числу невідомих. Знаходити розв’язок такої системи потрібно пошарово.
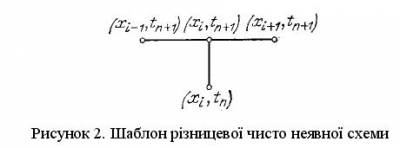
3. Неяні схеми. Чисто неявною різницевою схемою для рівняння теплопровідності (схемою з випередженням) називається різницева схема, що використовує шаблон зображений на рисунку 2.
Така схема має вигляд
Схема має перший порядок апроксимації по τ та другий − по h. Розв’язок системи (5) знаходиться так як і у випадку явної схеми, пошарово, починаючи з n=1. Але на відміну від явної схеми, потрібно розв’язати систему рівнянь
Цю систему можна розв’язати методом прогону.
Шеститочковою симетричною схемою називається різницева схема
для якої початкові та граничні умови задаються так як і в схемі (5). Ця схема використовує шеститочковий шаблон, зображений на рисунку 3.