Уравнение теплопроводимости для нестационарного случая
Обозначим через \(u=u(Mt,t)\) температуру в точке \(M\) однородного тела, ограниченного поверхностью \(S\) в момент времени \(t\). Известно, что количество теплоты \(dQ\) поглащаемой телом за время \(dt\) ,выражается равенством
$$dQ=k\cdot \frac{\partial u}{\partial n}dSdt,$$
где \(dS\) - элемент поверхности, \(k\) - так называемый коэфициент внутренней теплопроводности, \(\frac{\partial u}{\partial n}\) - производная функции \(u\) по направлению внешней нормали к поверхности \(S\)
Пример 1. Решить уравнение \(\frac{\partial u}{\partial t}=a^2\cdot \frac{\partial ^u}{\partial x^2}\) для следующего начального распределения температуры стержня:
$$u(x,t)\mid _{t=0}=f(x)=\begin{cases} & \text{ } u;x\in [x_1,x_2] \\ & \text{ } 0; \end{cases}$$
Стержень является бесконечным, поэтому решение запищется в виде интеграла Пуассона:
$$u(x,t)=\frac{1}{2a\sqrt {\pi t}}\cdot \int_{-\infty }^{+\infty }{f(\xi )\cdot e^{-(\xi -x)^2/(a^2t)}d\xi}.$$
Так как \(f(x)\) в интервале \([x_1,x_2]\) равна постоянной температуре \(u_0\) , а вне интервала температура равна нулю, то решение примет вид
$$u(x,t)=\frac{u_0}{2a\sqrt {\pi t}}\cdot \int_{-\infty }^{+\infty }{e^{-(\xi -x)^2/(a^2t)}d\xi}.$$
Полученый результат можно преобразовать к интервалу вероятностей.
$$\Phi (z)=\frac{2}{\sqrt \pi }\int_{0}^{z}{e^{-\mu ^2}d\mu }.$$
Действительно, полагая
$$x-\xi/(2a\sqrt y)=\mu ,d\xi =-2a\sqrt t\cdot d\mu,$$
получим
$$u(x,t)=-\frac{u_0}{\sqrt \pi }\int_{(x-x_1)/(2a\sqrt \pi )}^{(x-x_2)/(2a\sqrt \pi )}{e^{-\mu ^2}d\mu }=$$
$$=\frac{u_0}{\sqrt \pi }\int_{0}^{(x-x_1)/(2a\sqrt \pi )}{e^{-\mu ^2}d\mu }-\frac{u_0}{\sqrt \pi }\int_{0}^{(x-x_2)/(2a\sqrt \pi )}{e^{-\mu ^2}d\mu}.$$
Таким образом, решение выразится формулой
$$u(x,t)=\frac{u_0}{2}[\Phi (\frac{x-x_1}{2a\sqrt t})-\Phi (\frac{x-x_2}{2a\sqrt t})].$$
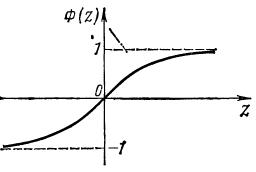
Графиком функции \(\Phi (z)\) является кривая, изображенная на рисунке.
Пример 2. Найти решение уравнения \(\frac{\partial u}{\partial t}=\frac{\partial ^2}{\partial x^2}\) удовлетворяющих начальному условию \(u\mid _{t=0}=f(x)=u_0,\) и краевому условию \(u\mid _{x=0}=0.\)
Здесь мы имеем дифференциальное уравнение теплопроводности для полубесконечного стержня. Решение, удовлетворяющее указанным условиям, иммет вид
$$u(x,t)=\frac{1}{2\sqrt {\pi t}}\int_{0}^{\infty }{u_0[e^{-(\xi -x)^2/(4t)}-e^{-(\xi +x)^2/(4t)}]}d\xi ,$$
или
$$u(x,t)=\frac{u_0}{2\sqrt {\pi t}}\int_{0}^{\infty }{[e^{-(\xi -x)^2/(4t)}-e^{-(\xi +x)^2/(4t)}]}d\xi .$$
Полагая \(x-\xi /(2\sqrt t)=\mu , d\xi =-2\sqrt td\mu,\) преобразуем первый интеграл, пользуясь интегралом вероятностей, т.е.
$$\frac{u_0}{2\sqrt {\pi t}}\int_{0}^{\infty }{e^{-(\xi -x)^2/(4t)}}d\xi=\frac{u_0}{\sqrt {\pi }}\int_{-\infty }^{x/(2\sqrt t)}{e^{-\mu }d\mu }=\frac{u_0}{2}{[1+\Phi (\frac{x}{2\sqrt t})]}.$$
Полагая \(x+\xi /(2\sqrt t)=\mu , d\xi =2\sqrt td\mu,\) получим
$$\frac{u_0}{2\sqrt {\pi t}}\int_{0}^{\infty }{e^{-(\xi +x)^2/(4t)}}d\xi=\frac{u_0}{\sqrt {\pi }}\int_{x/(2\sqrt t) }^{+\infty }{e^{-\mu }d\mu }=\frac{u_0}{2}{[1-\Phi (\frac{x}{2\sqrt t})]}.$$
Таким образом, решение принимат вид $$u(x,t)=u_0\cdot \Phi (\frac{x}{2\sqrt t}).$$