Площадь плоской фигуры, ограниченной областью D, находится по формуле

$$S=\int \int _{D}dxdy.$$

Если область D определена, например, неравенствами \(a\leq x\leq b, \varphi _1(x)\leq y\leq \varphi _2(x)\), то

$$S=\int_{a}^{b}{dx\int_{\varphi _1}^{\varphi _2}{dy}}. $$

Если область D в полярных координатах определена неравенствами \(\alpha \leq \theta \leq \beta , \varphi (\theta )\leq \rho \leq f(\theta ),\) то

$$S=\int \int _{D}\rho d\rho d\theta=\int_{\alpha }^{\beta }{d\theta }\int_{\varphi (\theta )}^{f(\theta )}{\rho d\rho} .$$

Пример 1. Вычеслить площадь фигуры, ограниченной линиями \(x=4y-y^2, x+y=6.\)

Найдем координаты точек пересечения заданных линий, решая систему уравнений \(x=4y-y^2\) и \(x+y=6\) (чертеж рекомендуется выполнить самостоятельно). В результате получим \(А(4;2), В(3;3)\). Таким образом получим,

$$S=\int \int _{D}dxdy=\int_{2}^{3}{dy}\int_{6-y}^{4y-y^2}{dx}=\int_{2}^{3}{x}\mid \begin{matrix} 4y-y^2 \\ 6-y \end{matrix} dy=$$

$$=\int_{2}^{3}{(-y^2+5y-6)dy}=[-\frac{1}{3}y^3+\frac{5}{2}y^2-6y]_2^3=\frac{1}{6}.$$

Пример 2. Найти площадь фигуры, ограниченной данными линиями : \(y=3/x, y=4e^x, y=3, y=4.\)

Решение. Построим область интегрирования D и находим площадь ограниченной области D (заштрихованая область).

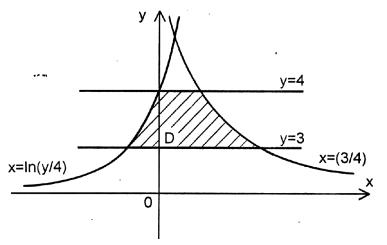
Пределы интегрирования для данной области определяются ее границами из неравенства \(3\leq y\leq 4; ln\frac{y}{4}\leq x\leq \frac{3}{y}\). Отсюда, применяя интегрирование по частям, получим

$$S=\int_{3}^{4}{dy}\int_{\ln (y/4)}^{3/y}{dx}=\int_{3}^{4}{\left[\frac{3}{y}-\ln \frac{y}{4}dy \right]}=\left[ 3\ln y-y\ln \frac{y}{4}+y\right]_3^4=1$$

Итак, площадь данной фигуры равна 1.

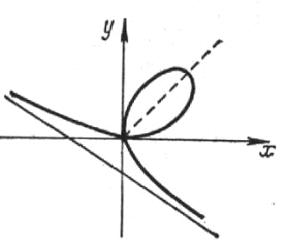
Пример 3. Найти площадь фигуры, ограниченной линией \(x^3+y^3=axy\)/

Решение. Область интегрирования есть площадь петли, симметричной относительно прямой \(x=y\). Преобразуем данное уравнение, используя полярные координаты.

Имеем :

$$r^3(\sin ^3\varphi +\cos ^3\varphi )=r^2\cdot a\cdot \sin \varphi \cdot \cos \varphi, или r=\frac{a\sin \varphi \cdot \cos \varphi }{\sin ^3\varphi +\cos ^3}.$$

Осью симметрии петли является ось \(\varphi =\pi /4\), поэтому область интегрирования разделим на две равные части по оси симметрии и искомая площадь будет равна удвоенному интегралу:

$$S=2\int \int _{D} rdrd\varphi =2\int_{0}^{\pi /4}{d\varphi }\int_{0}^{a\sin \varphi \cdot \cos \varphi /(\sin ^3\varphi +\cos ^3\varphi) }{rdr}=a^2\int_{0}^{\pi /4}{\frac{\sin ^2\varphi \cdot \cos ^2\varphi }{(\sin ^3\varphi +\cos ^3\varphi)}d\varphi }=$$

$$=a^2\int_{0}^{\pi /4}{\frac{tg^2\varphi \cdot \cos ^4\varphi }{\cos ^6\varphi (1+tg^3\varphi )^2}d\varphi }=\frac{a^2}{3}\int_{0}^{\pi /4}{\frac{3tg^2\varphi d(tg\varphi )}{(1+tg^3\varphi )2}}=$$

$$=\frac{a^2}{3}\int_{0}^{\pi /4}{\frac{d(1+tg^3\theta )}{(1+tg^3\theta )^2}}=-\frac{a^2}{3}\left[\frac{1}{1+tg^3\theta } \right]_0^\pi /4=\frac{a^2}{6}$$

Итак, площадь данной фигуры равна \(S=\frac{a^2}{6}\) .

2012-12-05 • Просмотров [ 23740 ]