\(a,\; b,\; c\) - стороны треугольника.
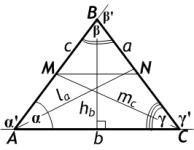
\(\alpha ,\; \beta ,\; \gamma\) - внутренние углы треугольника.
\(\alpha\, ' ,\; \beta\, ' ,\; \gamma\, '\) - внешние углы треугольника.
\(h_a,\; h_b\;h_c\) - высоты треугольника, опущенные из вершин треугольника на прямые, содержащие соответствующие противоположные стороны \(a,\; b,\; c\).
\(m_a,\; m_b\;m_c\) - медианы треугольника, соединяющие вершины треугольника с серединами противолежащих сторон \(a,\; b,\; c\).
\(l_a,\; l_b\;l_c\) - биссектрисы треугольника, соединяющие вершины треугольника с точками на противолежащих сторонах \(a,\; b,\; c\).
\(MN\) - средняя линия треугольника.
\(P\) - периметр треугольника.
\(p\) - полупериметр треугольника.
\(R\) - радиус окружности, описанной около треугольника.
\(r\) - радиус окружности, вписанной в треугольник.
\(S_{\triangle ABC}\) - площадь треугольника \(ABC\).

---

$$\frac{a}{\sin \alpha}=\frac{b}{\sin \beta}=\frac{c}{\sin \gamma}.$$

---

$$\begin{matrix} a^2=b^2+c^2-2bc\,\cos \alpha, \\ b^2=a^2+c^2-2ac\,\cos \beta,\\ c^2=a^2+b^2-2ab\,\cos \gamma. \end{matrix}$$

---

$$P=a+b+c,\;\;p=\frac{a+b+c}{2}.$$

---

$$S=\frac{1}{2}ah_a,\;\;S=\frac{1}{2}bh_b,\;\;S=\frac{1}{2}ch_c;$$ $$S=\frac{1}{2}ac\,\sin\beta ,\;\;S=\frac{1}{2}ab\,\sin\gamma ,\;\;S=\frac{1}{2}bc\,\sin\alpha;$$

---

$$\begin{matrix} a=c,\; \angle a=\angle \gamma,\\ h_b=m_b=l_b. \end{matrix}$$

---

$$\begin{matrix} a=b=c,\;\alpha =\beta =\gamma =60^\circ;\\ h_a=l_a=m_a,\;h_b=l_b=m_b,\;h_c=l_c=m_c;\;\\ R=\frac{a\sqrt 3}{3},\; r=\frac{a\sqrt 3}{6},\; S=\frac{a^2\sqrt 3}{4}. \end{matrix}$$

---

$$R=\frac{a}{2}=m_a,\;\;S=\frac{1}{2}bc,$$ $$\sin\gamma =\frac{c}{a},\;\;\cos\gamma =\frac{b}{a},\;\;\text{tg }\gamma =\frac{c}{b},$$ $$\sin\beta =\frac{b}{a},\;\;\cos\beta =\frac{c}{a},\;\;\text{tg }\beta =\frac{b}{c}.$$

---