Графическое интегрирование.
Пусть нам известен график функции \(y=f(x)\). Поставим задачу: геометрическими средствами, не прибегая к вычислениям, найти приближенное значение интеграла $$I=\int_{a}^{b}{f(x)dx}.$$
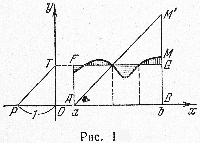
Будем предполагать, что масштаб по оси \(Ox\) равен масштабу по оси \(Oy\) и что полюс графика \(P\) находится на расстоянии единицы масштаба от начала координат: \(OP=1\) (рис.1). Проведем прямую \(FG\), параллельную оси \(Ox\) и пересекающую линию \(y=f(x)\) так, чтобы площадь полученного прямоугольника как можно меньше отличалась от площади нашей криволинейной трапеции. Для этого нужно, чтобы площадь, заключенная между линией и прямой \(FG\) и лежащая над прямой, по возможности точно равнялась площади, заключенной между линией и прямой и лежащей под прямой. продолжим прямую \(FG\) до пересечения с осью \(Oy\) в точке \(T\) и соединим эту точку с полюсом графика. Наконец, из точки \(A\) проведем прямую, параллельную \(PT\), до пересечения с прямой \(x=b\) в точке \(M'\).
Легко убедиться в том, что отрезок \(M'B\) изобраает искомую площадь, т.е. отрезок \(M'B\) содержит столько линейных масштабных единиц, сколько квадратных единиц содержит площадь криволинейной трапеции. В самом деле, из подобия треугольников \(POT\) и \(ABM'\) находим
|
$$\frac{BM'}{AB}=\frac{OT}{OP},$$
|
откуда
|
$$BM'=\frac{AB\cdot OT}{OP};$$
|
но \(OP=1\), а \(AB\cdot OT\) измеряет площадь трапеции.
Если интервал \([a,b]\) недостаточно мал, то проведение прямой \(FG\) на глаз может привести к ощутимой ошибке. Для того чтобы уточнить построение, разобьем интервал интегрирования на частичные интервалы (не обязательно равные между собой) и всю трапецию - на ряд трапеций, опирающихся на эти частичные интервалы. Точки деления выберем таким образом, чтобы каждый частичный интервал был интервалом монотонности подынтегральной функции и чтобы в числе точек деления находились все точки пересечения линии \(y=f(x)\) с осью \(Ox\). Если в каждом интервале линия незначительно отличается от прямой, то в качестве средних линий частичных трапеций можно брать просто ординаты в средних точках частичных интервалов. Тогда отпадает необходимость проводить на глаз вспомогательные линии. Практически обычно так и поступают.
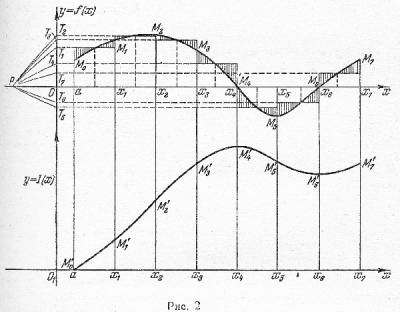
Последовательно для каждой из частичных криволинейных трапеций построим указанным выше путем отрезок, изображающий ее площадь. В целях ясности чертежа удобно откладывать этот отрезок не от данной оси \(Ox\), а от другой оси \(O_{1}x\), параллельной первой (рис.2). В точке \(x=a\) площадь трапеции, отсчитываемая от прямой \(x=a\), очевидно, равна нулю. Отметим на оси \(O_{1}x\) точку \(M'_{0}(a,0)\), она соответствует точке \(M_{0}\) линии \(y=f(x)\). До прямой \(x=x_{1}\) площадь трапеции равна площади первой частичной трапеции; она изобразится отрезком \(M_{1}x_{1}\), которой мы получим, если из точки \(M'_{0}\) проведем прямую, параллельную \(PT_{1}\), до пересечения с прямой \(x=x_{1}\) в точке \(M'_{1}\). Эта точка соответствует точке \(M_{1}\) на линии. Площадь трапеции до прямой \(x=x_{2}\) (т.е. значение интеграла, взятого от \(a\) до \(x_{2}\)) равна сумме (в алгебраическом смысле) площадей первой и второй частичных трапеций. Она изобразится отрезком \(M'_{2}x_{2}\), который получится, если из точки \(M'_{1}\) провести прямую, параллельную \(PT_{2}\), до пересечения с прямой \(x=x_{2}\) в точке \(M'_{2}\). Эта точка соответствует точке \(M'_{2}\) на линии. Продолжая так же дальше, построим последовательно точки \(M'_{3}, M'_{4}, ... ,\) соответствующие точкам \(M_{3}, M_{4}, ... \) линии. Ордината точки \(M'_{n}\), соответствующей точке \(M'_{n}[b,f(b)]\) линии, и даст нам искомое значение интеграла \(I\). Ясно, что чем больше точек деления, тем точнее получится построение.
Соединим полученные точки \(M'_{0},M'_{1},M'_{2},..., M'_{n}\) плавной линией. Ординаты этой линии, очевидно, приближенно изображают значения интеграла, взятого от \(x=a\) до соответствующих точек основания трапеции. Другими словами, эта линия является графиком функции, определяемой нашим интегралом с переменным верхним пределом: $$I(x)=\int_{a}^{x}{f(x)dx}.$$
Линия \(y=I(x)\) называется интегральной кривой функции \(y=f(x)\). Рассмотренное геометрическое построение интегральной кривой по графику подынтегральной функции называется графическим интегрированием.
Так же как и в случае графического дифференцирования, графическое интегрирование бывает наиболее удобным тогда, когда подынтегральная функция задается графически, а аналитическое ее выражение неизвестно. Это нередко встречается в практике, например, когда функция определяется графиком, записываемым самопишущим прибором.