Первообразная функция
Первообразной от функции \(f(x)\) называется функция \(F(x)\), производная которой равна данной функции: $$F'(x)=f(x).$$
Пусть \(y=x^{2}\). Для какой функции \(x^{2}\) служит производной? Очевидно, для \(\frac{x^{3}}{3}\): $$(\frac{x^{3}}{3})'=x^{2}.$$
Поэтому первообразной от \(x^{2}\) является функция \(\frac{x^{3}}{3}\). Но не только она. В самом деле, производной от \(\frac{x^{3}}{3}+5\), \(\frac{x^{3}}{3}-105\) и вообще от \(\frac{x^{3}}{3}+С\), где С - произвольная постоянная величина, будет также \(x^{2}\). Следовательно, любая функция \(\frac{x^{3}}{3}+С\) является первообразной от \(x^{2}\).
Две функции \(x^{2}\) и \(\frac{x^{3}}{3}+C\) при любой постоянной \(C\) находятся в таком соотношении друг к другу: первая является производной от второй, вторая - первообразной от первой.
Основная теорема о первообразных. Всякая непрерывная функция имеет бесчисленное множество первообразных, причем любые две из них отличаются друг от друга только постоянным слагаемым.
Примем, что любая непрерывная функция \(f(x)\) имеет первообразную \(F(x)\).
Но тогда, функция \(F(x)+C\) при всякой постоянной\(C\) будет также первообразной, так как $$[F(x)+C]'=F'(x)=f(x).$$
Итак, функция \(f(x)\) имеет бесчисленное множество первообразных.
Остается показать, что любые две первообразные от функции \(f(x)\) отличаются друг от друга лишь постоянным слагаемым. Пусть \(F(x)\) и \(\Phi(x)\) - две первообразные от \(f(x)\), тождественно не равные между собой. Имеем $$F'(x)=f(x), \Phi '(x)=f(x).$$
Вычитая одно равенство из другого, получим F'(x)-\Phi '(x)=0, т.е. \([F(x)-\Phi (x)]'=0\). Но если производная от некоторой функции тождественно равна нулю, то сама функция есть постоянная; следовательно, \(F(x)-\Phi (x)=C_{1}\) (где \(C_{1}\) - вполне определенная постоянная), что и требовалось доказать.
Таким образом, выражение \(F(x)+C\), где \(F(x)\) -какая-нибудь первообразная от \(f(x)\), а \(C\) - произвольная постоянная, охватывает все без исключения первообразные от \(f(x)\). Придавая различные численные значения \(C\), мы будем получать различные первообразные.
Геометрическая иллюстрация существования первообразной. Приведем теперь геометрическую иллюстрацию того факта, что любая непрерывная функция имеет первообразную.
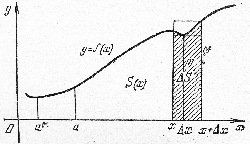
Рассмотрим график функции, изображенный на рисунке. Зафиксируем точку \(a\) и обозначим через \(S(x)\) площадь криволинейной трапеции с основанием \([a, x]\). Ясно, что, меняя \(x\), мы как-то изменяем и площадь криволинейной трапеции \(S(x)\). Найдем производную от функции \(S(x)\), исходя из определения производной $$S'(x)=\lim_{\Delta x\rightarrow 0}\frac{\Delta S}{\Delta x}.$$
Пусть \(x\) получит приращение \(\Delta x\); площадь \(S(x)\) получает при этом приращение \(\Delta S\). Геометрически ясно, что $$m\Delta x<\Delta S\leq M\Delta x,$$ где \(m\) и \(M\) - соответственно наименьшее и наибольшее значения функции \(f(x)\) в интервале \([x, x+\Delta x]\). Ведь \(m\Delta x\) - это площадь прямоугольника, целиком лежащего внутри фигуры, площадь которого обозначена \(\Delta S\), а M\Delta x - площадь прямоугольника, содержащего эту фигуру внутри себя. Деля все части неравенства на \(\Delta x\), получим $$m<\frac{\Delta S}{\Delta x}\leq M.$$
Так как \(f(x)\) - непрерывная функция, то при \(\Delta x\rightarrow 0\) и \(m\) и \(M\), являющиеся значениями функции в интервале \([x, x+\Delta x]\), будут стремиться к значению функции в точке \(x\), т.е. к \(f(x)\). По признаку существования предела отношения \(\frac{\Delta S}{\Delta x}\) будет стремиться к тому же пределу: $$\lim_{\Delta x\rightarrow 0}\frac{\Delta S}{\Delta x}=f(x).$$
Таким образом, \(S(x)\) действительно является первообразной от \(f(x)\).
Так же наглядно можно показать, что первообразных бесчисленное множество. Взяв за начальную не точку \(a\), а какую-нибудь другую точку \(a'\), мы получим новую функцию - площадь криволинейной трапеции с основанием \([a', x]\), которая отличается от \(S(x)\) на площадь трапеции с основанием \([a', a]\), т.е. на постоянную величину.
Интегрирование функций тесно связано с задачей отыскания площадей фигур, ограниченных кривыми линиями.