Если для решения некоторой массовой проблемы известен алгоритм, то для его реализации необходимо лишь четкое выполнение предписаний этоrо алгоритма. Автоматизм, необходимый при реализации алгоритма естественно приводит к мысли о передаче функции человека, реализующего алгоритм, машине. Идею такой машины предложили в тридцатые годы американский математик Э. Пост и английский математик А. Тьюринг.
Рассмотрим один из вариантов указанной машины, которая носит название машины Тьюринга.
Устройство машины Тьюринга включает в себя:
1. Внешний алфавит, то есть конечное множество символов \(A =\begin{Bmatrix} a_{0}, a_{1},a_{2}, ...,a_{n} \end{Bmatrix}\). В этом алфавите в виде слова кодируется та информация, которая подается в машину. Машина перерабатывает информацию, поданную в виде слова, в новое слово.
2. Внутренний алфавит машины, состоящий из символов \(q_{0},q_{1},q_{2},...,q_{m}\), п, л, н. Символы \(q_{0},q_{1},q_{2},...,q_{m}\) выражают конечное число состояний машины. Для любой машины число состояний фиксировано. Два состояния имеют особое назначение: \(q_{1}\) – начальное состояние машины, \(q_{0}\) – заключительное состояние (стоп-состояние). Символы п, л, н – это символы сдвига (вправо, влево, на месте).
3. Бесконечная в обе стороны лента (внешняя память машины). Она разбита на клетки. В каждую клетку может быть записана только одна буква. Пустую клетку будем обозначать символом \(a_{0}\).
4. Управляющая головка. Она передвигается вдоль ленты и может останавливаться напротив какой-либо клетки, то есть воспринимать символ или печатать символ. В одном такте работы машины управляющая головка может сдвигаться только на одну клетку (вправо, влево) или оставаться на месте.
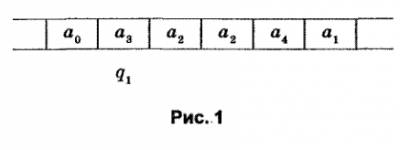
Каждое сведение, хранящееся на ленте, изображается конечным набором символов (букв) внешнего алфавита, отличного от \(a_{0}\). К началу работы машины на ленту подается начальное сведение (начальная информация). В этом случае управляющая головка, как правило, находится у крайнего левого знака с указанием начального состояния \(q_{1}\) (рис. 1) (начальная конфигурация).
Работа машины складывается из тактов, по ходу которых происходит преобразование начальной информации в промежуточные информации.
В качестве начальной информации на ленту можно подать любую конечную систему знаков внешнего алфавита (любое слово в этом алфавите), расставленную произвольным образом по ячейкам. Но в зависимости от того, какая была подана начальная информация, возможны два случая:
1. После конечного числа тактов машина останавливается (переходит в стоп-состояние \(q_{0}\)), и при этом на ленте оказывается изображенной информация \(B\). В таком случае говорят, что машина применима к начальной информации \(A\) и перерабатывает её в результирующую информацию \(B\).
2. Машина никогда не останавливается (не переходит в стоп-состояние). В таком случае говорят, что машина не применима к начальной информации \(A\).
В каждом такте работы машины она действует по функциональной схеме, которая имеет вид: $$a_{i}q_{j} \Rightarrow a_{v} \begin{Bmatrix} п,л,н \end{Bmatrix} q_{s}.$$
Здесь \(a_{i}, a_{v}\) – буквы внешнего алфавита; \(q_{i}, q_{s}\) – состояния машины; п, л, н – символы сдвига.
В зависимости от того, какая буква на ленте обозревается управляющей головкой (в нашей записи \(a_{i}\)) и в каком состоянии (в нашей записи \(q_{j}\)) находится машина, в данном такте вырабатывается команда, состоящая из трех элементов:
1. Буква внешнего алфавита, на которую заменятся обозреваемая буква (\(a_{v}\)).
2. Адрес внешней памяти для следующего такта \(\begin{Bmatrix} п,л,н \end{Bmatrix}\).
3. Следующее состояние машины (\(q_{s}\)).
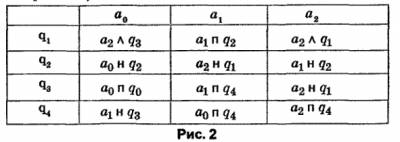
Совокупность всех команд образует программу машины Тьюринга. Программа представляется в виде двумерной таблицы и называется Тьюринговой функциональной схемой.
Пример такой схемы изображен на рис. 2 (машина Тьюринrа 1).
Ясно, что работа машины Тьюринга полностью определяется ее программой. Иными словами, две машины Тьюринга с общей функциональной схемой неразличимы, и различные машины Тьюринга имеют различные программы.
Для простоты изображения различных конфигураций машины Тьюринга будем в дальнейшем записывать информацию в виде слова, не изображая ленты и ее разбивки на клетки, а вместо изображения управляющей головки и состояния машины записывать только состояние машины.
Рассмотрим, как работает машина Тьюринга, заданная функциональной схемой 1.
Пример 1. Пусть начальная конфигурация имеет вид:
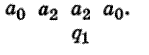
Так как управляющей головкой обозревается буква \(a_{2}\), а машина находится в состоянии \(q_{1}\), то машина вырабатывает команду \(a_{2} \wedge q_{1}\), и в результате получаем вторую конфигурацию
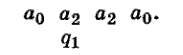
Очевидно, следующие конфигурации имеют вид:
Так как при пятой конфигурации машина находится в состоянии \(q_{0}\), то слово \(a_{2}a_{2}a_{2}\) является результатом.
Основная гипотеза теории алгоритмов
Машина Тьюринга дает один из путей уточнения понятия алгоритма. В связи с этим возникают вопросы: насколько общим является понятие машины Тьюринга? Можно ли считать, что способ задания алгоритмов с помощью машины Тьюринга является универсальным? Может ли всякий алгоритм задаваться таким образом?
На эти вопросы современная теория алгоритмов предлагает ответ в виде следующей гипотезы:
Всякий алгоритм может быть задан посредством тьюринговой функциональной схемы и реализован в соответствующей машине Тьюринга.
Эта гипотеза называется тезисом Тьюринга. Ее нельзя доказать, так как она связывает нестрогое определение понятия алгоритма со строгим определением понятия машины Тьюринга.
Эта гипотеза может быть опровергнута, если удастся привести пример алгоритма, который не может быть реализован с помощью тьюринговой функциональной схемы.
Однако все известные до сих пор алгоритмы могут быть заданы посредством тьюринговых функциональных схем.
Напомним также, что другие способы уточнения понятия алгоритма (понятие нормального алгоритма А. А. Маркова, понятие рекурсивного алгоритма (рекурсивной функции), введенного Чёрчем, Гёделем и Клини) оказались равносильными.
Этот факт является важным доводом в пользу сформулированной гипотезы.