Оценка интеграла. Теорема о среднем. Среднее значение функции.
1. Оценка интеграла. Укажем границы, между которыми наверняка заключено значение интеграла.
Теорема об оценке опеределенного интеграла. Значение определенного интеграла заключено между произведениями наименьшего и наибольшего значений подынтегральной функции на длину интервала интегрирования, т.е.
|
$$M(b-a)>\int_{a}^{b}{f(x)dx}>m(b-a),$$
|
$$b>a,$$
|
где \(M\) и \(m\) - соответственно наибольшее и наименьшее значения функции \(f(x)\) в интервале \([a,b]\): $$m\leq f(x)\leq M.$$
Доказательство. Возьмем две функции \(M-f(x)\) и \(m-f(x)\). Первая из них в интервале \([a,b]\) неотрицательна, вторая неположительна. Значит по теореме о знаке интеграла
|
$$\int_{a}^{b}{[M-f(x)]dx}>0$$
|
и
|
$$\int_{a}^{b}{[m-f(x)]dx}<0.$$
|
Применяя теоремы из пункта простейших свойств определенного интеграла и формулу \(\int_{a}^{b}{dx}=b-a\), получим
|
$$M(b-a)>\int_{a}^{b}{f(x)dx}$$
|
и
|
$$m(b-a)<\int_{a}^{b}{f(x)dx},$$
|
что и требовалось доказать. Из доказательства теоремы о знаке интеграла следует, что знаки неравенств могут перейти в знаки равенств только в том случае, когда функция \(f(x)\) постоянна.
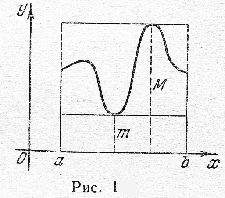
Геометрический смысл доказанных неравенств таков: площадь криволинейной трапеции больше площади прямоугольника с основанием, равным основанию трапеции, и высотой, равной наименьшей ординате трапеции, и меньше площади прямоугольника с тем же основанием и высотой, равной наибольшей ординате трапеции (рис. 1).
Находя границы для интеграла, мы, как говорят, производим его оценку. Может случиться, что весьма трудно или даже невозможно найти точное значение интеграла, а оценивая его, мы узнаем, хотя бы грубо, приближенное его значение. С такого рода оценками приходится довольно часто встречаться в математике.
Указанные в теореме об оценке определенного интеграла границы для интеграла тем более точны, чем короче интервал интегрирования и чем меньше линия \(y=f(x)\) отличается по положению от прямой, параллельной оси \(Ox\).
Пример 1. Оценим интеграл $$\int_{0}^{2}{\frac{5-x}{9-x^{2}}dx}.$$
Известными методами дифференциального исчисления находим, что наибольшее и наименьшее значения подынтегральной функции в интервале \([0, 2]\) равны соответственно \(0,6\) и \(0,5\). Значит, $$0,5(2-0)<\int_{0}^{2}{\frac{5-x}{9-x^{2}}dx}<0,6(2-0)$$
т.е. интеграл заключен между \(1\) и \(1,2\). Если считать, что он равен \(1,1\), то предельная абсолютная ошибка равна \(0,1\), а относительная \(\frac{0,1\cdot 100}{1,1}\approx 9%\).
Пример 2. Оценим интеграл $$\int_{\frac{\pi }{4}}^{\frac{\pi }{2}}{\frac{\sin x}{x}dx}.$$
Легко проверить, что подынтегральная функция в интервале \([\frac{\pi }{4}, \frac{\pi }{2}]\) убывает и, следовательно, $$\frac{\sin \frac{\pi }{2}}{\frac{\pi }{2}}\cdot \frac{\pi }{4}<\int_{\frac{\pi }{4}}^{\frac{\pi }{2}}{\frac{\sin x}{x}dx}<\frac{\sin \frac{\pi }{4}}{\frac{\pi }{4}}\cdot \frac{\pi }{4},$$
т.е. $$\frac{1}{2}<\int_{\frac{\pi }{4}}^{\frac{\pi }{2}}{\frac{\sin x}{x}dx}<\frac{1}{2}\sqrt{2}.$$
Таким образом, интеграл заключен между \(0,5\) и \(0,71\), что дает нам право считать его равным \(0,6\) с точностью до \(0,1\). Более точные приемы показывают, что приближенно он равен \(0,62\).
Оценка интеграла. Теорема о среднем. Среднее значение функции.
Продолжение здесь