Приближенные методы интегрирования.
Перейдем теперь к некоторым употребительным методам приближенного интегрирования, позволяющим находить приближенное значение определенного интеграла от любой непрерывной функции с практически достаточной точностью. Потребность в приближенном вычислении интеграла может возникнуть и тогда, когда не существует или неизвестен метод отыскания точного значения интеграла, и тогда, когда этот метод известен, но неудобен.Излагаемые приближенные численные методы основаны на следующем: рассматривая интеграл как площадь криволинейной трапеции, мы получим ее приближенное значение, т.е. приближенное значение интеграла, если вычислим площадь другой трапеции, ограничивающая линия которой по возможности мало отклоняется по положению от заданной линий. Вспомогательную линию при этом проводим так, чтобы получилась фигура, площадь которой легко вычисляется.
Дадим следующие правила численного интегрирования: 1) правило прямоугольников и правило трапеций; 2) правило параболических трапеций, называемое по имени его автора правилом Симпсона.
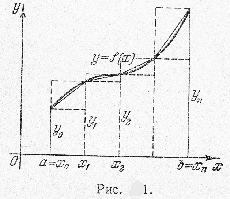
I. Правило прямоугольников и правило трапеций. Разделим интервал интегрирования \([a,b]\) на \(n\) равных частей (частичных интервалов) и заменим данную трапецию ступенчатой фигурой, состоящей из \(n\) прямоугольников, опирающихся на частичные интервалы, причем высоты этих прямоугольников равны значениям функции \(y=f(x)\) в начальных или в конечных точках частичных интервалов (рис.1). Значение площади этой фигуры и будет давать приближенное значение искомого интеграла \(I=\int_{a}^{b}{f(x)dx}.\) Результат будет тем более точен, чем больше взято число частичных интегралов.
Если обозначить значения функции \(f(x)\) в точках деления через \(y_{0}, y_{1}, ... , y_{n-1}, y_{n},\) т.е. положить \(y_{k}=f(x_{k})\), \(x_{k}=a+k\Delta x\), где \(\Delta x=\frac{b-a}{n}\), а \(k\) принимает значения \(0,1,2,...,n\), то, очевидно, будем иметь следующие формулы: $$I\approx \underline{I}=\Delta x(y_{0}+y_{1}+...+y_{n-1})$$
или $$I\approx \overline{I}=\Delta x(y_{0}+y_{1}+...+y_{n}).$$
Эти формулы и называются формулами прямоугольников.
Оставим разбиение интервала \([a,b]\) прежним, но заменим теперь каждую дугу линии \(y=f(x)\), соответствующую частичному интервалу, хордой, соединяющей конечные точки этой дуги. Таким образом, мы заменяем данную криволинейную трапецию \(n\) прямолинейными (рис.1). Геометрически очевидно, что площадь такой фигуры более точно выражает искомую площадь, чем площадь \(n\)-ступенчатой фигуры, составленной из прямоугольников.
Ясно, что площадь каждой трапеции, построенной на частичном интервале, соответсвующих этому интервалу прямоугольников. Суммируя все эти площади, получим $$I\approx I_{mp}=\frac{\underline{I}+\overline{I}}{2}=\Delta x(\frac{y_{0}+y_{n}}{2}+y_{1}+y_{2}+...+y_{n-1}).$$
Эта формула и носит название формулы трапеций.
Если функция \(f(x)\) монотонна, то величины \(\overline{I}\) и \(\underline{I}\) дают оценку интеграла значительно более точную, чем указанная в теореме об оценке определенного интеграла. При этом ясно, что если функция монотонно возрастает (этот случай как раз изображен на рис.1), то $$\overline{I}>I>\underline{I},$$
а если монотонно убывает, то, наоборот, $$\underline{I}>I>\overline{I}.$$
Беря в качестве приближенного значения интеграла значение, получаемое по формуле трапеций $$I\approx \frac{\underline{I}+\overline{I}}{2},$$
мы будем уверены, что абсолютная ошибка не превосходит абсолютной величины полуразности \(\overline{I}\) и \(\underline{I}\), т.е. $$\left|\Delta I\right| \leq \frac{\left| \underline{I}+\overline{I}\right|}{2}.$$
Пример 1. Найдем приближенное значение интеграла $$\int_{0}^{1}{\frac{dx}{1+x^{2}}}$$
и сравним найденные величины с его точным значением, равным \(arctg1=\frac{\pi }{4}\approx 0,785\). Пусть \(n=10\). Тогда \(\Delta x=0,1\); \(x_{k}=k\cdot 0,1\) \((k=0,1,2,...,10)\). Вычисляя значения функции (с точностью до \(0,001\)), получим
|
$$y_{0}=1,$$
|
$$y_{1}=\frac{1}{1+(0,1)^{2}}\approx 0,990,$$
|
|
$$y_{2}=\frac{1}{1+(0,2)^{2}}\approx 0,962,$$
|
$$y_{3}=0,917,$$
|
$$y_{4}=0,862,$$
|
$$y_{5}=0,8,$$
|
|
$$y_{6}=0,735,$$
|
$$y_{7}=0,671,$$
|
$$y_{8}=0,610,$$
|
$$y_{9}=0,552,$$
|
$$y_{10}=0,5.$$
|
Следовательно, $$\underline{I}=0,1(1+0,990+0,962+0,917+0,862+0,8+0,735+0,671+0,610+0,552)\approx 0,810.$$
Аналогично вычислим \(\overline{I}\): $$\overline{I}\approx 0,755.$$
В этом примере \(\overline{I}<\underline{I}\), так как функция убывающая. Таким образом, $$0,810>I>0,755.$$
Возьмем в качестве \(I\) значение $$I\approx \frac{0,755+0,810}{2}\approx 0,782.$$
При этом абсолютная ошибка не превосходит \(\frac{0,028\cdot 100}{0,782}\approx 3,6 \%\). Фактически же абсолютная ошибка составляет всего \(0,003.\)
Приближенные методы интегрирования. Продолжение здесь