Признаки сходимости несобственных интегралов с бесконечными пределами. Продолжение. Начало здесь
II. Признак сравнения I, сформулированный ранее, относится только к функциям, сохраняющим один и тот же знак в бесконечном интервале интегрирования (ясно, что исследование интеграла от отрицательной функции сводится к предыдущему). Более сложным оказывается исследование интегралов от функций, не сохраняющих постоянный знак, например таких, как \(\frac{\sin x}{x}\). Мы приведем сейчас один признак сходимости, позволяющий иногда сводить исследование к случаю положительных функций.
Если сходится интеграл \(\int_{a}^{\propto }{\left|f(x) \right|dx}\) (интеграл от абсолютной величины функции \(f(x)\)), то сходится и интеграл \(\int_{a}^{\propto }{f(x)dx}\). При этом интеграл\(\int_{a}^{\propto }{f(x)dx}\) называется абсолютно сходящимся.
Для доказательства образуем две вспомогательные функции \(f^{+}(x)\) и \(f^{-}(x)\), определив их следующим образом:
|
$$f^{+}(x)=f(x),$$
|
если
|
$$f(x)\geq 0$$
|
|
$$f^{+}(x)=0,$$
|
если
|
$$f(x)<0$$
|
|
$$f^{-}(x)=0,$$
|
если
|
$$f(x)>0$$
|
|
$$f^{-}(x)=f(x)$$
|
если
|
$$f(x)\leq 0.$$
|
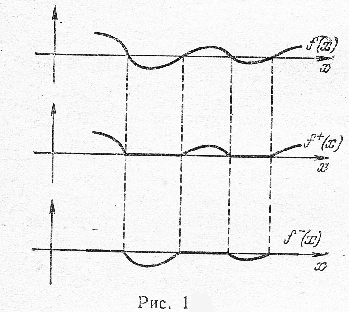
(Построение графиков функций \(f^{+}(x)\) и \(f^{-}(x)\) по заданной функции \(f(x)\) показано на рис.1). Ясно, что функции \(f^{+}(x)\) и \(f^{-}(x)\) неотрицательны и каждая из них не превосходит \(\left|f(x)\right|\). Так как по условию интеграл от \(\left|f(x)\right|\) сходится, то по признаку сравнения заключаем, что сходятся и интегралы \(\int_{a}^{\propto }{f^{+}(x)dx}\) и \(\int_{a}^{\propto }{[-f^{-}(x)]dx}\); изменив в последнем интеграле знак перед функцией, мы, очевидно, не нарушим его сходимости.
Но \(f(x)=f^{+}(x)+f^{-}(x)\), и раз сходятся интегралы от \(f^{+}(x)\) и \(f^{-}(x)\), то интеграл \(\int_{a}^{\propto }{f(x)dx}\) тоже сходится. Признак доказан.
Например, интегралы
|
$$\int_{0}^{\propto }{\frac{\cos x}{1+x^{2}}dx}$$
|
и
|
$$\int_{0}^{\propto }{\frac{\sin x}{1+x^{2}}dx}$$
|
абсолютно сходятся, так как подынтегральные функции по абсолютной величине не превосходят положительной функции \(\frac{1}{1+x^{2}}\), интеграл от которой сходится.
Если сходится интеграл \(\int_{-\propto }^{+\propto }{\left|f(x) \right|dx}\), то абсолютно сходятся и интегралы
|
$$\int_{-\propto }^{+\propto }{f(x)\cos x dx}$$
|
и
|
$$\int_{-\propto }^{+\propto }{f(x)\sin x dx},$$
|
так как модули подынтегральных функций, очевидно, не превосходят \(\left| f(x)\right|\).
Если интеграл от \(\left| f(x)\right|\) расходится, то об интеграле от \(f(x)\) на одном этом основании еще ничего сказать нельзя: он может расходиться, а может и сходиться. В последнем случае (т.е. когда интеграл от \(f(x)\) сходится, а интеграл от \(\left| f(x)\right|\) расходится) говорят, что \(\int_{a}^{\propto }{f(x)dx}\) сходится условно (не абсолютно).
Примером этого служит интеграл Дирихле \(\int_{0}^{\propto }{\frac{\sin x}{x}dx}\). Можно доказать, что этот интеграл сходится, а интеграл от модуля подынтегральной функции расходится. Таким образом, интеграл Дирихле сходится условно. Его величина вычислена специальными приемами: $$\int_{0}^{\propto }{\frac{\sin x}{x}dx}=\frac{\pi }{2}.$$