Оценка интеграла. Теорема о среднем. Среднее значение функции. Продолжение. Начало здесь

     Обобщение теоремы об оценке интеграла. Интегрирование неравенств. Справедлива следующая более общая теорема чем теорема об оценке определенного интеграла.
     Теорема 1. Если в каждой точке \(x\) интервала \([a,b]\) $$\psi (x)\leq f(x)\leq \varphi (x),$$
то

$$\int_{a}^{b}{\psi (x)}dx<\int_{a}^{b}{f(x)dx}<\int_{a}^{b}{\varphi (x)dx},$$

$$b>a.$$

     Это значит, что неравенство между функциями влечет неравенство того же смысла между их определенными интегралами, или, говоря коротко, неравенства можно интегрировать. Дифференцирование неравенства может привести к нелепым результатам. Например, из неравенства \(M>f(x)\), конечно, не следует, что \(f'(x)<0\).
     Доказательство теоремы немедленно следует из применения к неравенствам \(f(x)-\varphi (x)\leq 0\) и \(f(x)-\psi (x)\geq 0\) теоремы о знаке интеграла. Опять знак неравенства между интегралами переходит в знак равенства тогда и только тогда, когда функции тождественно равны между собой.
     В частном случае, когда \(\varphi (x)\) тождественно равно \(M\), а \(\psi (x)\) тождественно равно \(m\), получаем теорему об оценке определенного интеграла.
     С помощью теоремы 1 легко получается важное неравенство. При любом \(x\) $$-\left|f(x) \right|\leq f(x)\leq \left|f(x) \right|.$$
(Если \(f(x)>0\), то правая часть неравенства превращается в равенство, а левая часть очевидна; если \(f(x)<0\), то наоборот.) Тогда $$-\int_{a}^{b}{\left|f(x) \right|dx}\leq \int_{a}^{b}{f(x)dx}\leq \int_{a}^{b}{\left|f(x) \right|dx}$$
или $$\left|\int_{a}^{b}{f(x)dx} \right|\leq \int_{a}^{b}{\left|f(x) \right|dx}.$$
     Модуль интеграла не превосходит интеграла от модуля функции.
     Теорема о среднем - важное свойство определенного интеграла
     Теорема о среднем. Внутри интервала интегрирования \([a, b]\) существует хотя бы одно значение \(x=\xi\), для которого

$$\frac{\int_{a}^{b}{f(x)dx}}{b-a}=f(\xi ).$$

(1)

     Доказательство. В силу теоремы об оценке определенного интеграла имеем $$m<\frac{\int_{a}^{b}{f(x)dx}}{b-a}\leq M$$
и, значит, $$\frac{\int_{a}^{b}{f(x)dx}}{b-a}=\mu,$$
где \(\mu,\) - некоторое число, заключенное между наименьшим (\(m\)) и наибольшим (\(M\)) значениями функции \(f(x)\) в интервале \([a, b]\), т.е. \(m<\mu\leq M\). Но \(f(x)\), будучи непрерывной функцией, обязательно принимает хотя бы один раз каждое значение, лежащее между \(m\) и \(M\). Следовательно, при некотором \(\xi\in(a,b)\) функция \(f(x)\) получит значение, равное \(\mu\), т.е. \(f(\xi )=\mu\), что и требовалось доказать.
     Из равенства (1) находим

$$\int_{a}^{b}{f(x)dx}=f(\xi)(b-a),$$

$$a<\xi\leq b.$$

эта формула позволяет теорему о среднем высказать в такой форме:
     Определенный интеграл от непрерывной функции равен произведению значения этой функции в некоторой промежуточной точке интервала интегрирования на длину интервала.
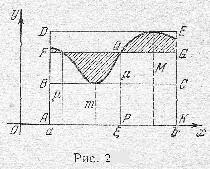
     Дадим наглядное пояснение теоремы. При движении прямой, параллельной оси \(Ox\) (рис. 2), вверх от положения \(BC\) площадь прямоугольника \(ABCK\) будет непрерывно возрастать от величины, большей ее. Очевидно, при некотором промежуточном положении прямой - обозначим его через \(FG\) - площадь прямоугольника \(AFGK\) окажется в точности равной площади трапеции \(S\). Так как при этом движении прямая постоянно пересекает линию, ограничивающую трапецию, то и в положении \(FG\) найдется одна или несколько (на рис. 2 две) точек пересечения \(Q\); абсцисса любой точки пересечения и будет требуемым по теореме значением \(\xi\).

     Оценка интеграла. Теорема о среднем. Среднее значение функции. Продолжение здесь

---