Плотность распределения
    Пусть имеется непрерывная случайная величина \(X\) с функцией распределения \(F(x)\), которую мы предположим непрерывной и дифференцируемой. Вычислим вероятность попадания этой случайной величины на участок от \(x\) до \(x+\Delta x\):

$$P(x< X< x+\Delta x)=F(x+\Delta x)-F(x)$$ т. е. приращение функции распределения на этом участке. Рассмотрим отношение этой вероятности к длине участка, т. е. среднюю вероятность, приходящуюся на единицу длины на этом участке, и будем приближать \(\Delta \) к нулю. В пределе получим производную от функции распределения: $$\lim_{\Delta x\rightarrow 0} {\frac{F(x+\Delta x)-F(x)}{\Delta}}=\acute{F}(x)$$ Введем обозначение: $$f(x)=\acute{F}(x)$$     Функция \(f(x)\) — производная функции распределения — характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения непрерывной случайной величины \(X\). Иногда функцию \(f(x)\) называют также «дифференциальной функцией распределения» или «дифференциальным законом распределения» величины \(X\).
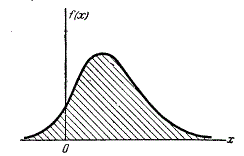
    Термины «плотность распределения», «плотность вероятности» становятся особенно наглядными при пользовании механической интерпретацией распределения; в этой интерпретации функция \(f(x)\) буквально характеризует плотность распределения масс по оси абсцисс (так называемую «линейную плотность»). Кривая, изображающая плотность распределения случайной величины, называется кривой распределения (рис.1). Рис.1
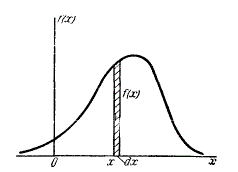
    Рассмотрим непрерывную случайную величину \(X\) плотностью распределения \(f(x)\) и элементарный участок \(dx\), примыкающий к точке \(x\)(рис.2). Вероятность попадания случайной величины \(X\) на этот элементарный участок (с точностью до бесконечно малых высшего порядка) равна \(f(x)dx\). Величина \(f(x)dx\) называется элементом вероятности. Геометрически это есть площадь элементарного прямоугольника, опирающегося на отрезок \(dx\)(рис.2). Рис.2
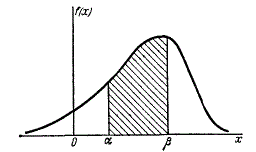
    Выразим вероятность попадания величины \(X\) на отрезок от \(\alpha\) до \(\beta\) (рис.3) через плотность распределения. Очевидно, она равна сумме элементов вероятности на всем этом участке, т. е. интегралу: $$P(\alpha < X< \beta )=\int_{\alpha }^{\beta }{f(x)dx}$$ Рис.3
    Укажем основные свойства плотности распределения.
1. Плотность распределения есть неотрицательная функция: $$f(x) >0$$ Это свойство непосредственно вытекает из того, что функция распределения \(F(x)\) есть неубывающая функция.
2. Интеграл в бесконечных пределах от плотности распределения равен единице: $$\int_{-\infty}^{+\infty}{f(x)dx}=1$$ Это следует из того, что \(F(+\infty)=1\);
    Геометрически основные свойства плотности распределения означают, что:
1. Вся кривая распределения лежит не ниже оси абсцисс;
2. Полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.

---