Понятие о системы случайных величин
В практических применениях теории вероятностей очень часто приходится сталкиваться с задачами, в которых результат опыта описывается не одной случайной величиной, а двумя или более случайными величинами, образующими комплекс или систему. Например, точка попадания снаряда определяется не одной случайной величиной, а двумя: абсциссой и ординатой — и может быть рассмотрена как комплекс двух случайных величин. Аналогично точка разрыва дистанционного снаряда определяется комплексом трех случайных величин.
При стрельбе группой из п выстрелов совокупность точек попадания на плоскости может рассматриваться как комплекс или система \(2n\) случайных величин: \(n\) абсцисс и \(n\) ординат точек попадания. Осколок,
образовавшийся при разрыве снаряда, характеризуется рядом случайных величин: весом, размерами, начальной скоростью, направлением полета и т. д. Условимся систему нескольких случайных величин
\(X, Y,..., W\) обозначать \((X, Y,..., W)\).
Свойства системы нескольких случайных величин не исчерпываются свойствами отдельных величин, ее составляющих: помимо этого, они включают также взаимные связи (зависимости) между случайными величинами.
При рассмотрении вопросов, связанных с системами случайных
величин, удобно пользоваться геометрической интерпретацией системы.
Например, систему двух случайных величин \((X, Y)\) можно изображать случайной точкой на плоскости с координатами \(X\) и \(Y\) (рис. 1). Аналогично система трех случайных величин может быть изображена случайной точкой в трехмерном пространстве. Часто бывает удобно говорить о системе \(n\) случайных величин как о «случайной точке б пространстве \(n\) измерений». Несмотря на то, что последняя интерпретация не обладает непосредственной наглядностью, пользование ею дает некоторый выигрыш в смысле общности терминологии и упрощения записей.
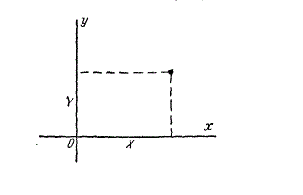
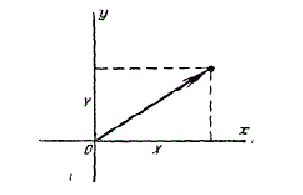
Часто вместо образа случайной точки для геометрической интерпретации системы случайных величин пользуются образом случайного вектора. Систему двух случайных величин при этом
рассматривают как случайный вектор на плоскости \(xOy\), составляющие которого по осям представляют собой случайные величины \(X, Y\)(рис. 2). Система трех случайных величин изображается случайным
вектором в трехмерном пространстве, система \(n\) случайных величин — случайным вектором в пространстве \(n\) измерений. При этом теория систем случайных величин рассматривается как теория случайных векторов.
Не всегда студенту удается разобраться самостоятельно с теорией вероятности. Тогда приходится обращаться за помощью к преподавателю. Причем, есть интересная статистика: около 20% студентов отличников не справляются с решением задач по теорверу и комбинаторике. Причина проста - в этом предмете другая логика.