Ряд распределения. Многоугольник распределения

    Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, неизвестно заранее – какое именно. Различают случайные величины прерывного (дискретного) и непрерывного типа. Возможные значения прерывных величин могут быть заранее перечислены. Возможные значения непрерывных величин не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток.
    Примеры прерывных случайных величин:
1) число появлений герба при трех бросаниях монеты (возможные значения \(0, 1, 2, 3)\);
2) число попаданий в самолет, достаточное для вывода его из строя.
    Примеры непрерывных случайных величин:
1) абсцисса точки попадания при выстреле;
2) ошибка измерителя высоты.
    Рассмотрим непрерывную случайную величину \(X\) с возможными значениями \(x_{1}, x_{1}, ..., x_{n}\). Каждое из этих значений возможно, но не достоверно, и величина \(X\) может принять каждое из них с некоторой вероятность. В результате опыта величина \(X\) примет одно из этих значений, т.е. произойдет одно из полной группы несовместных событий: $$ \begin{cases}X=x_{1}\\......\\ X=x_{n}\end{cases} $$     Обозначим вероятность этих событий буквами \(p\) с соответствующими индексами:

\(P(X=x_{1})=p_{1};\)  \(P(X=x_{2})=p_{2};\)...  \(P(X=x_{n})=p_{n};\)
    Так как несовместные события образуют полную группу, то $$\sum_{i=1}^{n}{p_{i}}=1,$$ т.е. сумма вероятностей всех возможных значений случайной величины равна единице. Эта суммарная вероятность каким-то образом распределена между отдельными значениями. Случайная величина будет полностью описана с вероятностной точки зрения, если мы зададим это распределение, т.е. в точности укажем, какой вероятностью обладает каждое из событий. Этим мы установим так называемый закон распределения случайной величины.
    Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Про случайную величину мы будем говорить, что она подчинена данному закону распределения.
    Установим форму, в которой может быть задан закон распределения прерывной случайной величины \(X\). Простейшей формой задания этого закона является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности:

\(x_{i}\)	\(x_{1}\)	\(x_{2}\)	\(...\)	\(x_{n}\)
\(p_{i}\)	\(p_{1}\)	\(p_{2}\)	\(...\)	\(p_{n}\)

    Такую таблицу мы будем называть рядом распределения случайной величины \(X\).
    Чтобы придать ряду более наглядный вид, часто прибегают к его графическому изображению: по оси абсцисс откладываются возможные значения случайной величины, а по оси ординат – вероятности этих значений. Для наглядности полученные точки соединяются отрезками прямых. Такая фигура называется многоугольником распределения.     Многоугольник распределения, так же как и ряд распределения, полностью характеризует случайную величину; он является одной из форм закона распределения.
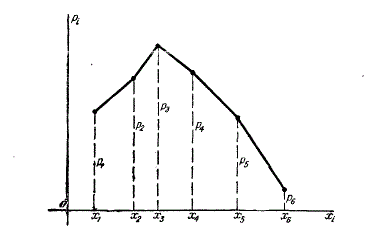
    Иногда удобной оказывается так называемая «механическая» интерпретация ряда распределения. Представим себе, что некоторая масса, равна единице, распределена по оси абсцисс так, что в \(n\) отдельных точках \(x_{1}, x_{2},..., x_{n}\) сосредоточены соответственно массы \(p_{1}, p_{2},..., p_{n}\). Тогда ряд распределения интерпретируется как система материальных точек с какими-то массами, расположенных на оси абсцисс.

---